Предмет: Алгебра,
автор: olgarud2407
Рішіть будь-ласка систему рівнянь ❤️
Приложения:
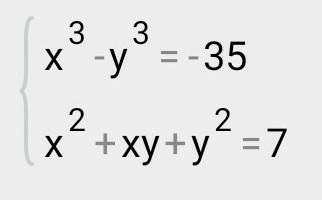
Ответы
Автор ответа:
1
Ответ:
Если будут какие-нибудь вопросы — задавайте. Если мой ответ оказался полезен, нажимайте «спасибо» и отмечайте его как «лучший ответ».
Похожие вопросы
Предмет: Химия,
автор: FinitiYiti681
Предмет: Литература,
автор: nazirkanybekov
Предмет: Математика,
автор: kartinabeznogova
Предмет: Математика,
автор: дина373
Предмет: История,
автор: Typikw2