Question

Изобразите на координатной плоскости фигуру, координаты (х;у) всех точек которой является решение системы неравенств

{х^2 + у^2 <= 16
{х - у >= 1

Answer 1

$x^2+y^2\leq 16$

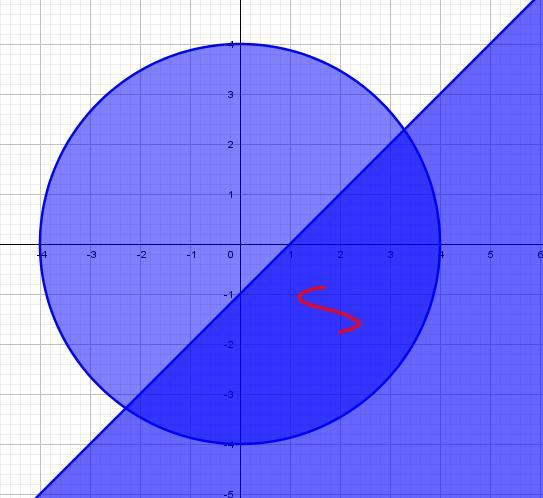
Представляет собой окружность с центром (0;0) и R = 4. Область - лежащий внутри окружности.

$x-y\geq 1$

Строится прямая y = x - 1, которая проходит через точку (0;-1), (1;0). Область - нижняя часть прямой.

Пересечение этих двух неравенств есть решением системы.

Answer 2

Ответ и решение во вложении

Граница первого неравенства = окружность, а второго - прямая у=х-1, которая получается путем сдвига на единицу вниз биссектрисы первого и третьего координатных углов. т.е. прямая у=х-1.