Предмет: Алгебра,
автор: Аноним
решить систему....................................................................................................................
Приложения:
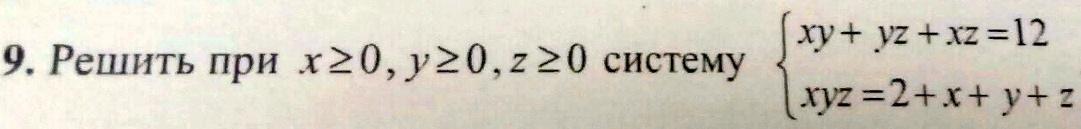
Ответы
Автор ответа:
5
Задание. Решить при x ≥0, y≥0, z ≥0 систему
{xy+yz+zx = 12
{xyz = 2 + x + y + z
Решение:
Известно, что среднее гармоническое не превышает среднее геометрическое, т.е.
Известно, что среднее геометрическое не превышает среднее арифметическое, т.е.
Тогда откуда
Равенство возможно только при x = y = z = 2
Аноним:
Поправил немного
Похожие вопросы
Предмет: Английский язык,
автор: Masyanchic
Предмет: Русский язык,
автор: bluetea66666
Предмет: Українська мова,
автор: solomiamatskiv
Предмет: Математика,
автор: генрих31
Предмет: Математика,
автор: sungayla