Question

Помогите, пожалуйста, решить задачу!
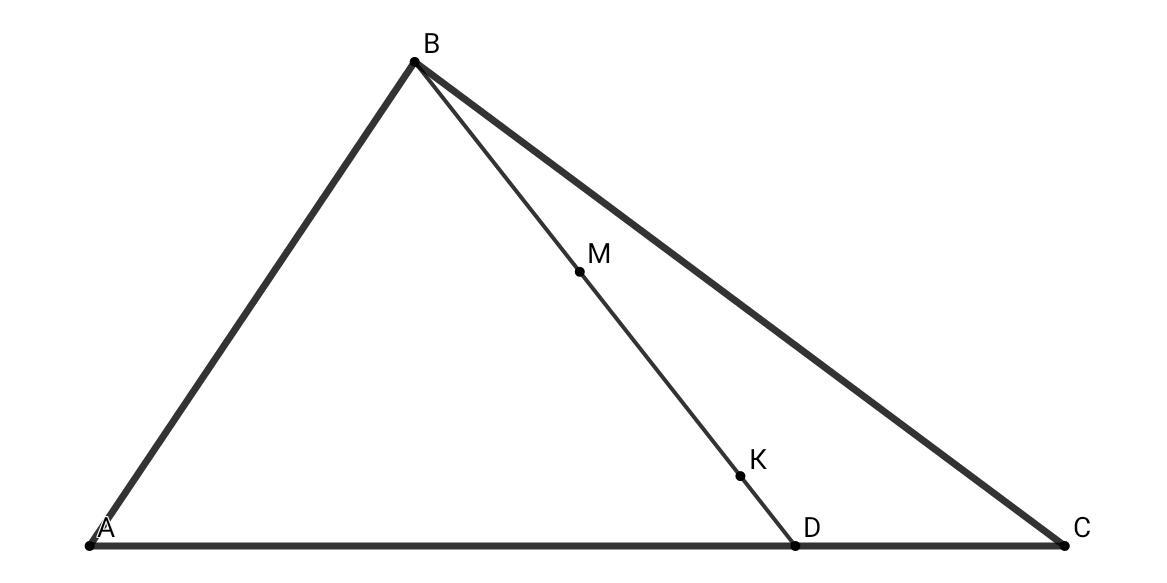
В треугольнике со сторонами BC= 8 см,AC=12 см,AB=7 см. Точка D делит сторону AC в отношении 3:1 считая от точки A. В треугольники ABD и BDC вписаны окружности. Найти расстояние между точками касания отрезка BD этими окружностями.
Спасибо!

Answer 1

AC = 12 см, AD/DC = 3/1  ⇒  AD = (3/4)•АС = 9 см, DC = 12 - 9 = 3 см

Пусть М и К - это точки касания вписанных окружностей в ΔАВD и ΔBDC соответственно, тогда по известной теореме про значения отрезков касательных:

Отрезок касательной равен разности полупериметра треугольника и противолежащей ей стороны

MD = p₁ - AB   и   KD = p₂ - BC

p₁ и р₂ - это полупериметры ΔABD и ΔBDC соответственно

Искомое рассстояние MK = MD - KD = p₁ - AB - (p₂ - BC) = p₁ - p₂ + BC - AB = (1/2)•(AB + AD + BD) - (1/2)•(BD + BC + DC) + ВС - АВ =  (1/2)•(AD + BC - DC - AB) = (1/2)•(9 + 8 - 3 - 7) = (1/2)•7 = 3,5

Значит, МК = 3,5 см

Ответ: 3,5 см