Предмет: Математика,
автор: ponguell
Помогите решить пожалуйста
Приложения:
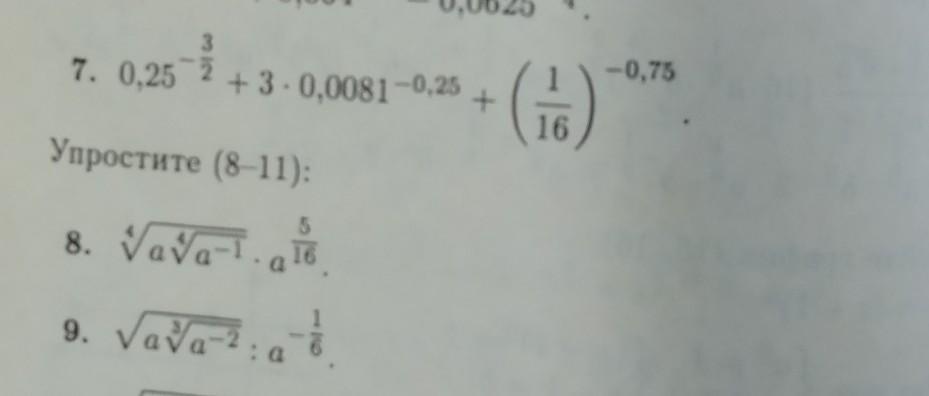
Ответы
Автор ответа:
1
Ответ:
iosiffinikov:
Коллеги, но ведь в двух последних, мне кажется ошибки (я , кстати, в первом сначала ошибся). Так (a^(-1/4)*a)^1/4=(a^(3/4))^1/4=a^(3/16)
Проверьте, пожалуйста!
да, походу, я лоханулся
сейчас представил в форме степеней и понял что получается а^(1-1/4) = a^3/4
спасибо, что подсказали
Автор ответа:
2
Ответ:
7) 26
8) a^(1/2) (корень квадратный из а)
9) a^(1/3) (корень кубический из а)
Пошаговое объяснение:
7) 0,25^(3/2)=0,5^3=0,125 0,25^(-3/2)=8
0,0081^(-0,25)=1/(0,3)=10/3
(1/16)^(3/4)=(1/2)^3=0,125 (1/16)^(-3/4)=8
8+3*10/3+8=26
8) (a^(-1/4)*a)^(1/4)=(a^(3/4))^(1/4)=a^(3/16)
a^(3/16)*a^(5/16)=a^(8/16)=a^(1/2)
9) ((a^(-2))^(1/3)*a)^(1/2)=(a^(-2/3)*a)^(1/2)=
(a^(1/3))^(1/2)=a^(1/6)
a^(1/6)*a^(1/6)=a^(1/3)
Похожие вопросы
Предмет: Физика,
автор: vovchikmazniuk
Предмет: География,
автор: tymurdvo
Предмет: Биология,
автор: bozhenapiskunowa02
Предмет: Математика,
автор: помромиль
Предмет: Математика,
автор: вика2660