Question

Задание 1. Вероятность того, что баскетболист попадет в кольцо при одной
попытке равна 0.1. Баскетболист совершил 3 бросков. Составить закон распределения количества попаданий. Построить многоугольник распределения.
Вычислить математическое ожидание, дисперсию, среднее квадратическое
отклонение.

Answer 1

Случайная величина Х - количество попаданий в кольцо. Случайная величина распределена по биномиальному закону. Вероятность успеха в одном испытании p = 0.1, тогда q = 1 - p = 0.9

1) Вероятность того, что баскетболист не попадает в кольцо ниразу

$P(X=0)=q^3=0.9^3=0.729$

2) Вероятность того, что баскетболист попадет один раз

$P(X=1)=C^1_3pq^2=3\cdot 0.1\cdot 0.9^2=0.243$

3) Вероятность того, что баскетболист попадет два раза

$P(X=2)=C^2_3p^2q=3\cdot 0.1^2\cdot 0.9=0.027$

4) Вероятность того, что баскетболист попадет три раза

$P(X=3)=p^3=0.1^3=0.001$

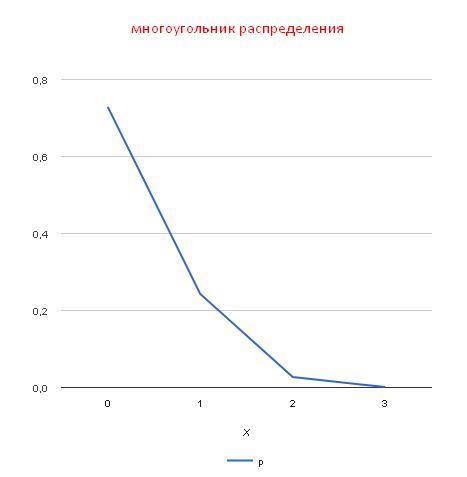
Закон распределения случайной величины X:

Xi       0            1               2            3

Pi    0.729     0.243      0.027      0.001

Математическое ожидание случайной величины X:

$MX=\displaystyle \sum_ix_ip_i=0\cdot 0.729+1\cdot 0.243+2\cdot 0.027+3\cdot 0.001=0.3$

Иначе мат. ожидание можно подсчитать, если Х - распределена по биномиальному закону то $MX=np=3\cdot 0.1=0.3$

Дисперсия случайной величины X:

$DX=MX^2-(MX)^2=\displaystyle \sum_ix_i^2p_i-0.3^2=0^2\cdot 0.729+1^2\cdot 0.243+\\ \\ +2^2\cdot 0.027+3^2\cdot 0.001-0.09=0.27$

Иначе: $DX=npq=3\cdot 0.1\cdot 0.9=0.27$

Среднее квадратическое отклонение:

$\sigma (X)=\sqrt{DX}=\sqrt{0.27}=0.3\sqrt{3}\approx 0.52$