Предмет: Геометрия,
автор: Мозговина12
ПОМОГИТЕ С РЕШЕНИЕМ ,ОЧЕНЬ ПРОШУ!!!!!!!❤❤❤
По координатам точек А, В, С для указанных векторов найти:
а) модуль вектора а
б) скалярное произведение векторов а, b
в) проекцию вектора с на вектор d
г) координаты точки М, делящей отрезок перпендикулярно в отношении α/β
Приложения:
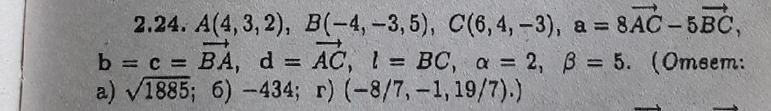
Simba2017:
это же не школа..
в) 37/sqrt(30) :)
Не понятен пункт г) координаты точки М, делящей отрезок перпендикулярно в отношении α/β. Какой отрезок делит точка М???
пропорционально наверное...
но какой отрезок...
BC
Да, это ВС. Он обозначен l.
Ответы
Автор ответа:
37
a) Длина вектора а:
б) Скалярное произведение векторов a,b
в) Проекция вектора с на вектор d
г) Координаты точки М, делящей отрезок BC отношении 2:5
Точка М имеет координаты
Спасибо ВАМ огрооомное)))ВЫ очень меня выручили)
Автор ответа:
9
Ответ и решение во вложении
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: galinaprijmak7
Предмет: Английский язык,
автор: sofikidun
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: halazi