Предмет: Геометрия,
автор: zeka1560
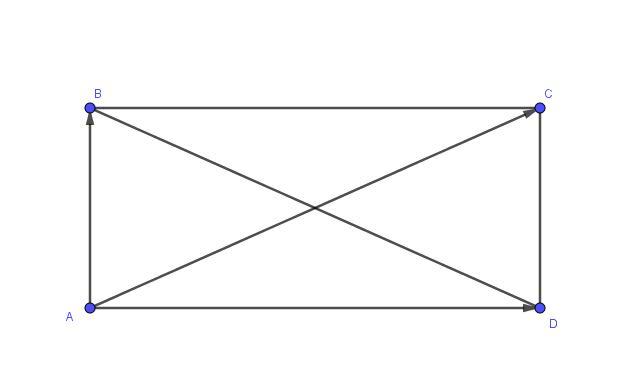
Дан прямоугольник ABCD доказать что |AB+AD|=|AB-AD| это вектора
Ответы
Автор ответа:
2
Векторы - перпендикулярны, то их скалярное произведение равно 0, то есть
Значит
Следовательно, или это
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: shhaaargg
Предмет: Геометрия,
автор: shhaaargg
Предмет: Алгебра,
автор: dasha23456789hb
Предмет: Литература,
автор: шрам0951
Предмет: Литература,
автор: HarryPotter55555