В трапеции
ABCD с меньшим основанием BC=3
и боковыми сторонами AB=12 и CD=15
биссектриса угла ADC
пересекает сторону AB
в её середине. Найдите основание AD
и высоту трапеции.
Ответы
Ответ:
Пошаговое объяснение:
Дано:
BC=3
AB=12
CD=15
AH=HB
∠ADH=HDC
Найти:
AD - большее основание трапеции АВСD
BA - высота трапеции АВСD
Решение:
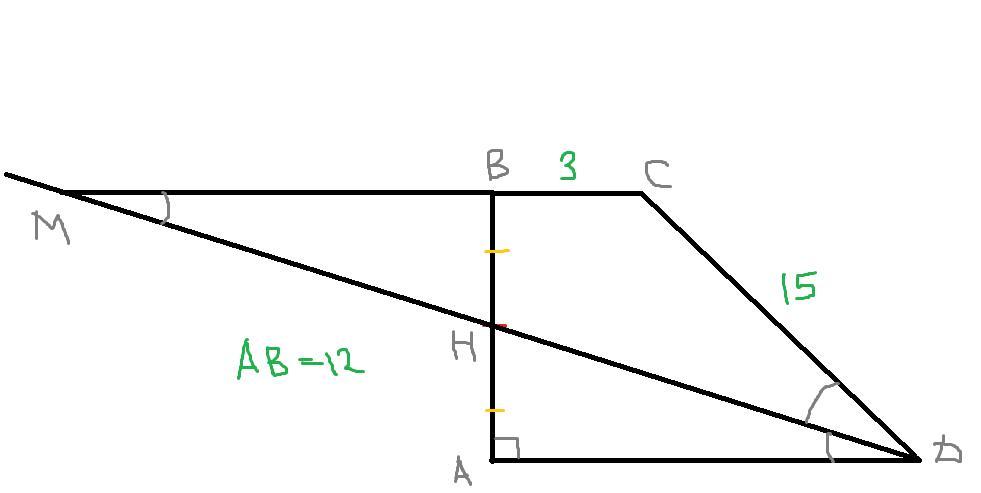
В трапеции АВСD биссектрису HD продолжим до точки M . При этом продолжим меньшее основание ВС у трапеции ABCD,также до точки M пересечения с продолжением биссектрисы HD. Исходя из сделанного дополнительного построения получаем,что углы ∠ADH=∠HDC=∠CMD . Так как ∠ADH=∠HDC=∠CMD,то треугольник MCD является равнобедренным,то есть MC=CD и поэтому сторона MC=15.
Если нам известно,что MC=15,а малое основание ВС=3,то MB=12.
Так как нам известно из условия,что AH=HB ,то опираясь на признаках равенства треугольников получаем,что ΔMBH=ΔHAD,следовательно MB=AD=12.
Высота в это случае равна AB,то есть AB=h=12
Ответ: Большее основание трапеции ABCD - AD=12
Высота трапеции ABCD равна 12