Question

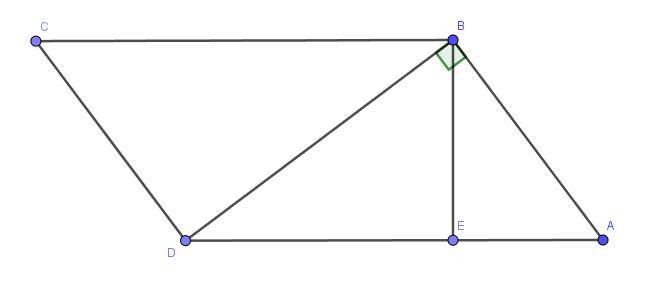
В параллелограмме ABCD диагональ BD перпендикулярна стороне AB. Из вершины прямого угла B проведена высота BE к стороне AD. Найдите площадь параллелограмма ABCD, если BE=6 см, а отрезок AE=3 см

Answer 1

Рассмотрим прямоугольный треугольник BDA

Высота, проведенная из вершины прямого угла к гипотенузе AD есть среднее пропорциональное между проекциями катетов

$BE^2=ED\cdot AE~~~\Rightarrow~~ ED=\dfrac{BE^2}{AE}=\dfrac{6^2}{3}=12~_{\sf CM}$

Площадь параллелограмма ABCD: $S=AD\cdot BE=(12+3)\cdot 6=90$ см²

Ответ: 90 см²