Предмет: Алгебра,
автор: artmov1994
Решите пожалуйста с объяснением
Приложения:
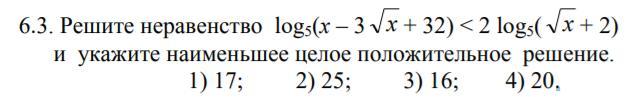
Ответы
Автор ответа:
1
Ответ: x=17 .
Объяснение:
artmov1994:
Спасибо огромное, это не подскажите как решить? https://znanija.com/task/32698096
И в одз вопрос, кореньx+2>0 можно же представить как x>4?
нет, нельзя...(корень х +2)>0 --> (корехнь х)> -2 - это неравенство верно для всех x>=0, так как сам (корень х)>=0
тем более (корень х)> k.,juj jnhbwfntkmyjuj xbckf
(корень х)> любого орицательного числа
Похожие вопросы
Предмет: Физика,
автор: dariatk02
Предмет: Физика,
автор: angelina8317
Предмет: Русский язык,
автор: materialgirl
Предмет: Литература,
автор: legser4
Предмет: Химия,
автор: vikaagentvika