Предмет: Геометрия,
автор: Evgeniya1204
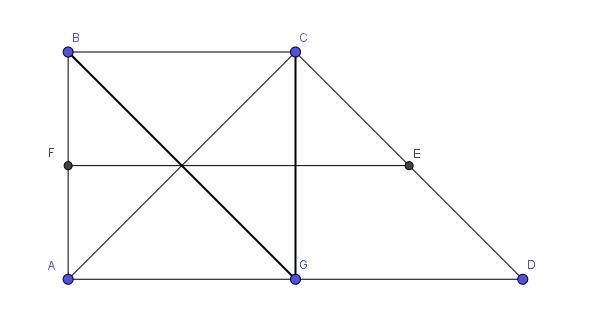
У прямокутній трапеції діагональ, проведена з вершини тупого кута, дорівнює бічній стороні. Знайдіть відношення середньої лінії цієї трапеції до її більшої основи
Ответы
Автор ответа:
3
Достроив до параллелограмма получим что
, но так как треугольник
- равнобедренный, то
- высота, медиана и биссектриса, следовательно,
Средняя линия трапеции равна полусумме оснований
Таким образом,
Ответ: 3 : 4.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: nastymi33
Предмет: Литература,
автор: evgeniykolomoiets
Предмет: История,
автор: hshdhfufh
Предмет: География,
автор: megalani03
Предмет: Алгебра,
автор: varclayen