Предмет: Математика,
автор: FederikoAndreo
1. Найти область определение функции
Z= 
2. Вычислить значение производной сложной функции
U= где
где  при t = 0
при t = 0
Ответы
Автор ответа:
1
Пошаговое объяснение:
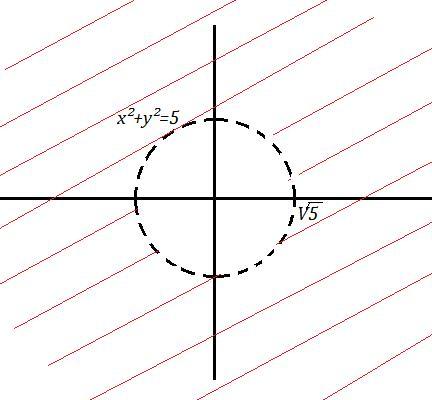
Обл. определения ф-ции является часть плоскости, которая находится вне круга с центром в точке (0,0) и .
P.S. Граница круга ( окружность ) в ООФ не входит .
Приложения:
FederikoAndreo:
А графики можите подсказать?
указана окружность с центром в (0,0) и R=sqrt5... чкртить окружность не умеете ??????????
туплю, спасибо большое, задал ещё один вопрос, буду очень балагодарен если ответите и на него
добавила рисунок...
Огромное вам спасибо, если-бы не вы я бы не закрыл вышку
учитесь... данные задания вовсе не сложные...
первое задание вообще - школа...
Да уже поздно её учить, закрыть как-то нужно что-бы на 3 курс перейти, если вам не трудно можите помочь со 2 вопросом?
мне уже некогда, ухожу...
Все равно, спасибо вам большое, возможно как освободитесь вот ссылка: https://znanija.com/task/32652879
Похожие вопросы
Предмет: Литература,
автор: danan8584
Предмет: География,
автор: katyaTolochko
Предмет: Геометрия,
автор: hshs12hshshs
Предмет: География,
автор: megalani03
Предмет: Алгебра,
автор: varclayen