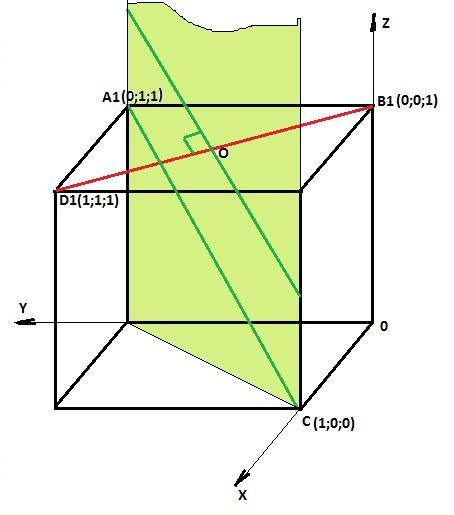
В кубе ABCDA1B1C1D1 найдите угол между прямыми B1D1 и A1C
Ответ должен получиться 90 градусов
Ответы
Ответ:
Угол равен 90°
Объяснение:
Определение: Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым".
Прямая А1С принадлежит плоскости диагонального сечения куба. Прямая B1D1 принадлежит плоскости верхнего основания куба. Эти плоскости взаимно перпендикулярны. Значит, если мы проведем прямую параллельную А1С в плоскости, содержащей плоскость диагонального сечения АА1С1С так, что эта прямая будет пересекаться с прямой B1D1, то угол между ними будет равен 90 градусов.
Или координатным методом: привяжем к вершине В куба прямоугольную систему координат.
Примем сторону куба равной 1.Тогда имеем точки:
А1(0;1;1), С(1;0;0), B1(0;0;1), D1(1;1;1) и соответственно векторы:
А1С{1;-1;-1} и B1D1{1;1;0}. Угол между векторами определяется по его косинусу, который равен скалярному произведению этих векторов, деленному на произведение их модулей.
Скалярное произведение векторов А1С и B1D1 равно сумме произведений соответствующих координат, то есть:
1·1 + (-1)·1 + (-1)·0 = 0. Этого нам достаточно, так как если скалярнле произведение векторов равно нулю, эти вектора перпендикулярны друг другу.