Предмет: Алгебра,
автор: poii14
Срочно! Упростить выражение
Приложения:
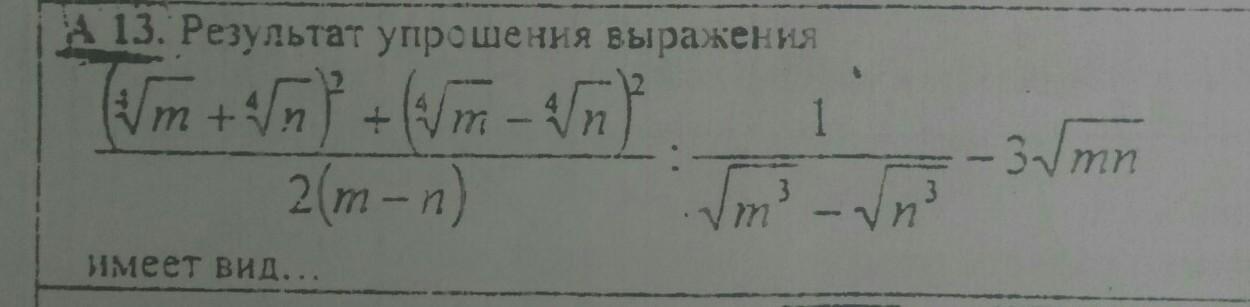
Ответы
Автор ответа:
0
Итак
Похожие вопросы
Предмет: Русский язык,
автор: lovescccam
Предмет: Алгебра,
автор: polinapolina369
Предмет: Геометрия,
автор: rotornay87oxiiuw
Предмет: Физика,
автор: roza2002
Предмет: География,
автор: Blaser228