Предмет: Геометрия,
автор: toporovelisei
К окружности с центром в точке О проведены касательные DC и FC (A и B - точки касания). Определите другие углы треугольника ABC, если угол BOA равен 116 градусов.
Ответы
Автор ответа:
4
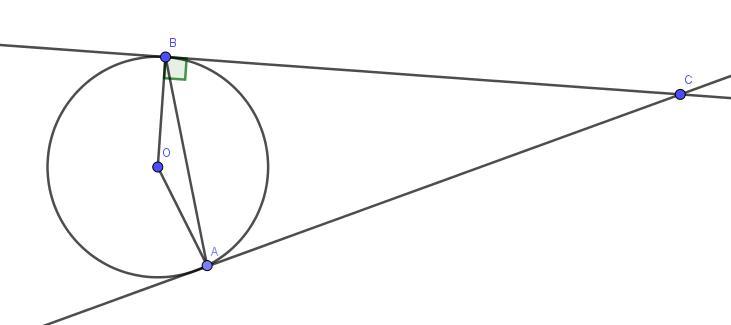
К окружности с центром в точке О проведены касательные AC и BC (A и B - точки касания). Определите другие углы треугольника ABC, если угол BOA равен 116 градусов.
Решение:
Треугольник AOB - равнобедренный, так как AO = OB как радиусы окружности, тогда ∠OAB = ∠OBA = (180° - ∠BOA)/2 = 32°.
Радиус проведенный к касательной перпендикулярен.
∠OAC = 90°, тогда ∠BAC = ∠ABC = 90° - ∠OAB = 90° - 32° = 58°
∠BCA = 180° - 2∠ABC = 180° - 2 · 58° = 64°
Ответ: 58°; 58°; 64°.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: moldanaminecraft
Предмет: Русский язык,
автор: Rampaban
Предмет: Математика,
автор: nnik63314
Предмет: Математика,
автор: Димаэтояяяя
Предмет: Математика,
автор: dashagromtseva