Предмет: Геометрия,
автор: pand53
В треугольнике АСЕ известны:
АС = 6 см,
АЕ =

см, .
<CAE=45°
Найдите: а) СЕ;
б)sin <ACE
Ответы
Автор ответа:
1
Ответ:
a)√26 см
б)
Объяснение:
a) по теореме косинусов:
CE=√(АС²+АЕ²-2*АС•АЕ•соs(CAE))
СЕ=√(36+50-60)=√26(см)
б) по теореме синусов:
sin(ACE)=(sin(CAE)•AE)/CE
sin(ACE)=5/√26
Приложения:
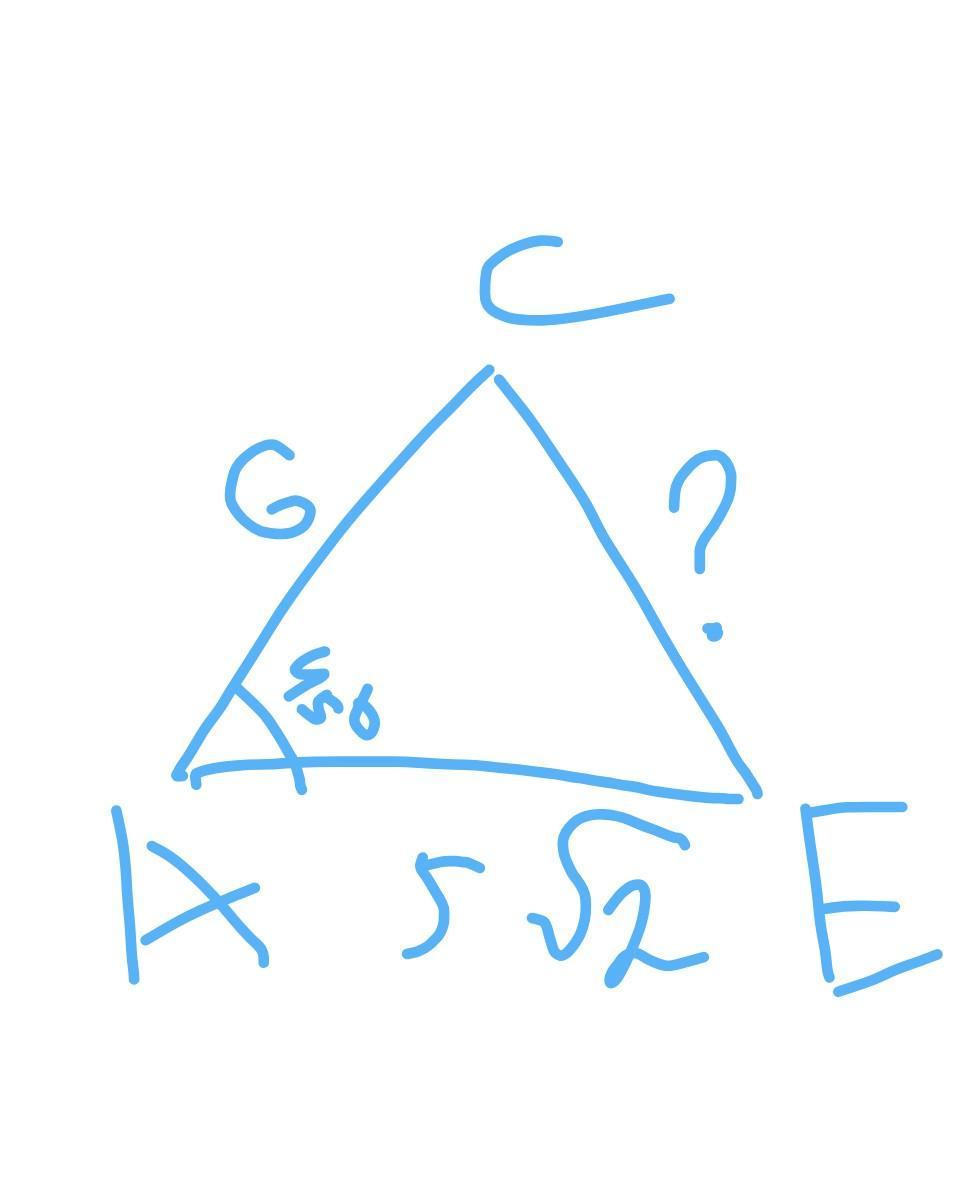
pand53:
спасибо
Похожие вопросы
Предмет: География,
автор: okercrew
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: dashakuza223
Предмет: Алгебра,
автор: nessai1