Question

В прямоугольный треугольник ABC (C = 90°) вписана окружность с ценром O и радиусом √3. Угол OBC =30°, найдите площадь треугольника ABC.

Answer 1

Ответ:

(9+6$\sqrt{3}$)ед$^{2}$

Объяснение:

Answer 2

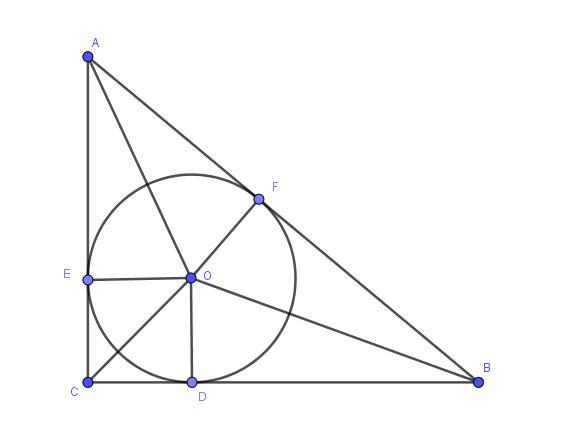
Так как центр окружности является точкой пересечения биссектрис, то ∠ABC = 2∠OBC = 60°.

OE = OD = CE = CD = √3. Из прямоугольного треугольника DOB:

tg∠OBD = OD/BD  ⇒  tg30° = √3/BD   ⇒  1/√3 = √3/BD

BD = √3 · √3 = 3, тогда BC = CD + BD = 3 + √3 =

Теперь из прямоугольного треугольника ABC

tg∠ABC = AC/BC  ⇒   AC = BCtg60° = (3+√3) · √3 = √3(1+√3)

$S=\dfrac{AC\cdot BC}{2}=\dfrac{\sqrt{3}(1+\sqrt{3})\cdot 3(1+\sqrt{3})}{2}=3\sqrt{3}(2+\sqrt{3})$ кв. ед.