Question

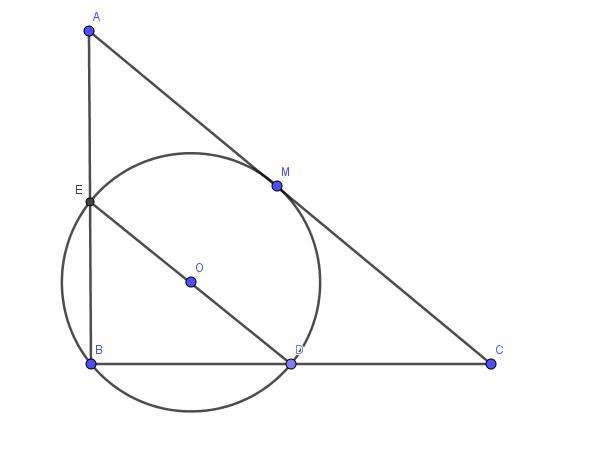
В треугольнике ABC со сторонами АВ = корень 14, BC = 2, через вершину В и середину стороны ВС (точку D) проведена окружность, касающаяся стороны AC и пересекающая АВ в точке Е. Найти отношение AE: EB, если ED - диаметр окружности.
Помогите пожалуйста ​

Answer 1

Поскольку вписанный угол B опирается на диаметр, то ∠B = 90°.

D - середина BC, следовательно, BD = CD = BC/2 = 1.

Из прямоугольного треугольника ABC по т. Пифагора :

$AC=\sqrt{AB^2+BC^2}=\sqrt{14+4}=\sqrt{18}=3\sqrt{2}$

По теореме о касательной и секущей, мы имеем:

$CM^2=CD\cdot BC=1\cdot 2~~~\Rightarrow~~~ CM=\sqrt{2}$

$AM^2=AE\cdot AB\\ \\ (AC-CM)^2=AE\cdot AB\\ \\ (3\sqrt{2}-\sqrt{2})^2=AE\cdot \sqrt{14}\\ \\ 4\cdot 2=AE\sqrt{14}\\ \\ AE=\dfrac{8}{\sqrt{14}}=\dfrac{8\sqrt{14}}{14}=\dfrac{4\sqrt{14}}{7}$

Тогда $BE=AB-AE=\sqrt{14}-\dfrac{4\sqrt{14}}{7}=\dfrac{7\sqrt{14}-4\sqrt{14}}{7}=\dfrac{3\sqrt{14}}{7}$

Следовательно, $AE:EB=\dfrac{4\sqrt{14}}{7}:\dfrac{3\sqrt{14}}{7}=4:3$

Ответ: 4 : 3.