Предмет: Математика,
автор: Grishan4ik1
Докажите, что при любом натуральном n число 3^3n+2+5*2^3n+1 кратно 19.
Приложения:
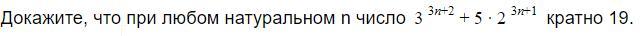
aastap7775:
нормально условие запиши
Сделал
Ответы
Автор ответа:
2
Пусть n = 1, тогда:
Так как при некотором n это число действительно кратно 19, то пусть некоторое n = k, при котором это число кратно, тогда исследуем это число при n = k+1, получим:
Первое слагаемое делится на 19, так как мы предположили, что при n = k это выражение делится на 19, а второе слагаемое делится на 19 согласно основной теоремы арифметики.
Автор ответа:
2
3³ⁿ⁺² + 5×2³ⁿ⁺¹ = 9×27ⁿ + 10×8ⁿ ≡ 9×8ⁿ + 10×8ⁿ = 19×8ⁿ ≡ 0×8ⁿ = 0 (mod 19). ⇒ ∀n ∈ ℕ: 3³ⁿ⁺² + 5×2³ⁿ⁺¹ кратно 19.
Q.E.D.
Похожие вопросы
Предмет: Русский язык,
автор: kurvanzanhodzasev209
Предмет: Французский язык,
автор: yyaau74
Предмет: Геометрия,
автор: mamagold1213
Предмет: Литература,
автор: polinka20005