Предмет: Математика,
автор: xajiliroxu
Помогите пожалуйста. Не получается решить.
Приложения:
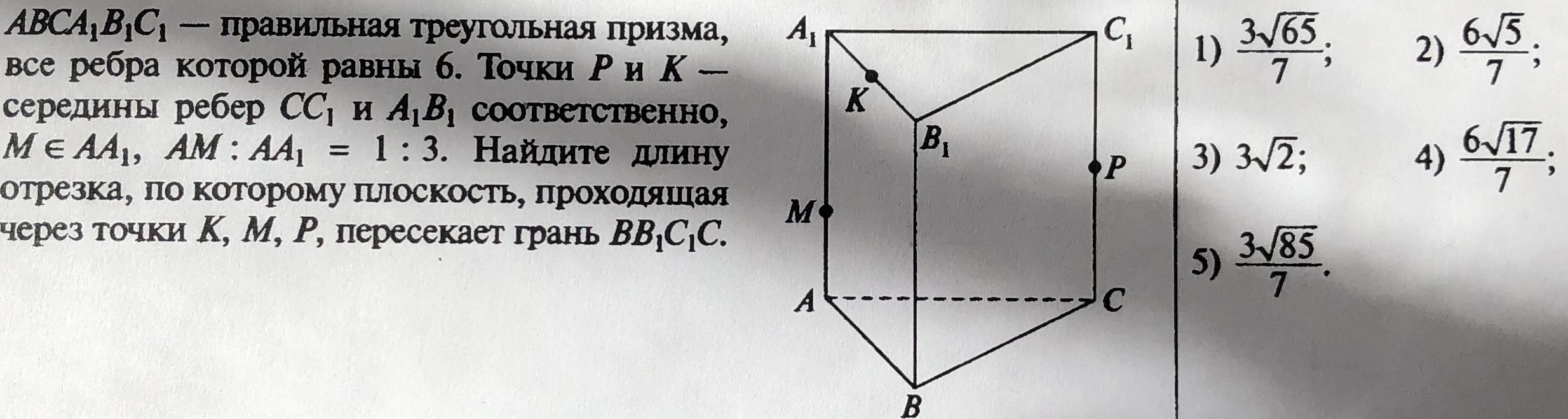
Аноним:
ответ: 5)
Ответы
Автор ответа:
0
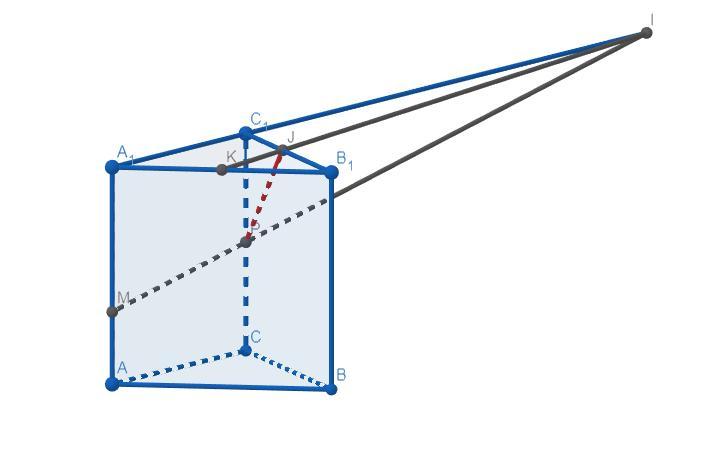
MP ∩ A₁C₁ = I,
IK ∩ B₁C₁ = J.
PJ - искомый отрезок.
ΔPC₁I подобен ΔMA₁I:
По теореме Менелая:
По теореме Пифарога:
Ответ: 5.
Приложения:
Похожие вопросы
Предмет: История,
автор: kostacuprov34
Предмет: Окружающий мир,
автор: averchenkoksiusha
Предмет: Физика,
автор: cuteSeagull
Предмет: Математика,
автор: wolf122
Предмет: Математика,
автор: MimitosPlay