Question

У рівнобедреному трикутнику ABC основа AC дорівнює 18. Через точку О - середину висоти BD - проведено промені АО і СО, які перетинають бічні сторони в точках М і К. Знайти довжину відрізка МК.
* * *
В равнобедренном треугольнике ABC основание AC равна 18. Через точку О - середину высоты BD - проведено лучи АО и СО, которые пересекают боковые стороны в точках М и К. Найти длину отрезка МК.

Answer 1

Ответ: 6 (ед. длины)

Объяснение:

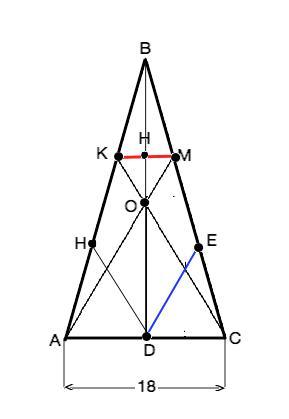
  Проведем DE║AM.  В треугольнике АМС отрезки АD=DC ( т.к. ВD медиана ∆ АВС и делит АС пополам). DE параллельна АМ и является средней линией ∆ АМС.⇒ СЕ=ЕМ.

В ∆ ВDE отрезок ОМ  - средняя линия ( ВО=ОD, и ОМ║DE). ⇒ ВМ=МЕ=ЕС.  

Аналогично, проведя из D параллельно СК прямую DH доказывается равенство ВК=КН=НА. ⇒ Так как ∆ АВС равнобедренный,  ВК=ВМ. Треугольник КВМ подобен ∆ АВС по пропорциональным сторонам и углу между ними. Коэффициент подобия k=ВМ:ВС=1/3, откуда КМ=АС:3=18:3=6 (ед. длины).

Answer 2

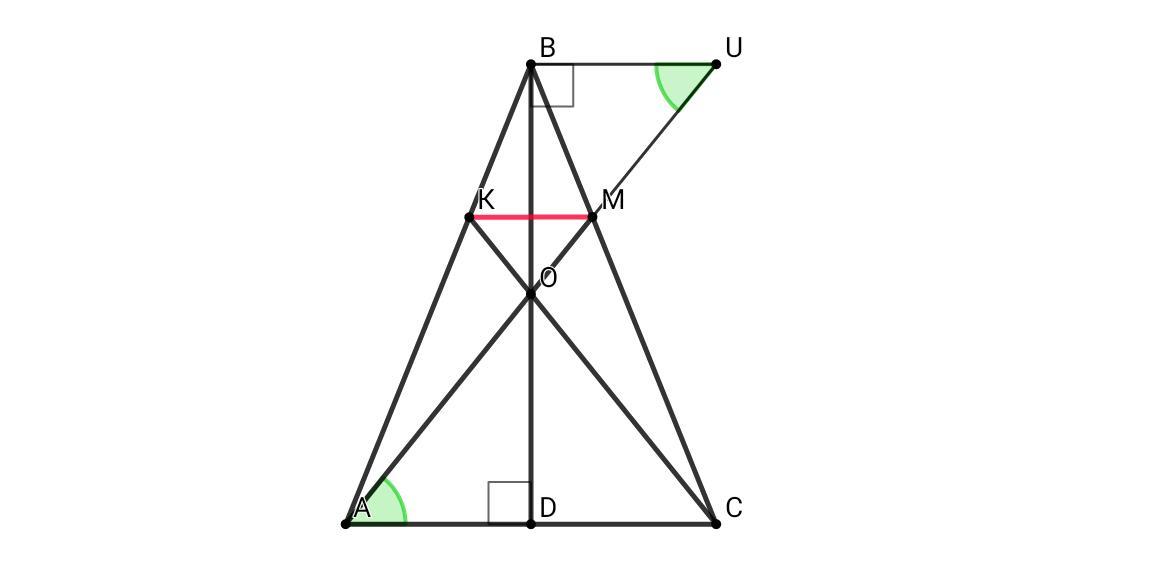
ΔАВС - равнобедренный, BD - высота, медиана, биссектриса ⇒ AD = DC = 18/2 = 9

Продолжим прямую АМ до пересечения с прямой BU, параллельной прямой АС ⇒ ΔАОD = ΔBOU по катету и острому углу (ВО = OD - по условию, ∠AOD = ∠BOU - как вертикальные углы) ⇒ AD = BU = 9

ΔВМU подобен ΔАМС по двум углам (∠UAC = ∠BUA - как накрест лежащие углы при BU || AC и секущей АU ; ∠BMU = ∠AMC - как вертикальные углы)

AM/MU = BM/MC = BU/AC = 9/18 = 1/2

Аналогично доказывается, что ВК/КА = 1/2, продлив прямую КС до пересечения с прямой BU

ИЛИ по теореме Менелая для ΔВСD и секущей АМ ⇒ CM/MB • BO/OD • AD/AC = 1 ;  CM/MB • 1 • (9/18) = 1 ⇒ CM/MB = 2

Аналогично для ΔABD и секущей КС ⇒ AK/KB = 2

Значит, BK/KA = BM/MC = 1/2 ⇒ ΔКВМ подобен ΔАВС по двум пропорциональным сторонам и равному углу между ними: МК || АС

ВК/АВ = ВМ/ВСМ= МК/АС ;   ВМ/ВС = МК/АС

1/3 = КМ/18  ⇒  КМ = 18/3 = 6

ОТВЕТ: 6