Предмет: Алгебра,
автор: larex6202
помогите решить уравнение
Приложения:
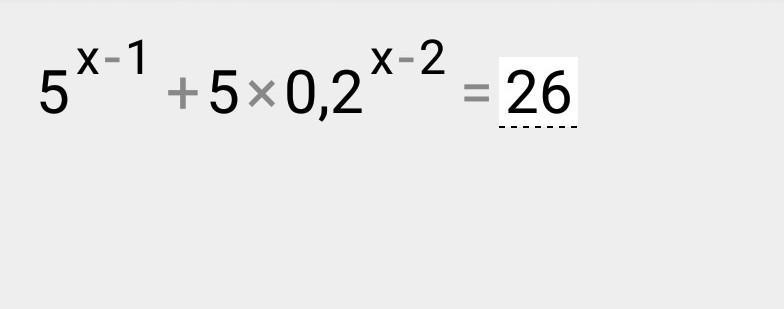
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Представим 0.2 как 1/5, или 5 с отрицательной степеню.
Получим:
Проведем замену:
Тогда:
Можно решить это уравнение дискриминантом, но числа, которые получатся, будут очень большими для вычислений, поэтому воспользуемся теоремой Виета. 625 - это произведение корней данного квадратного уравнения, иначе говоря, каждый из корней квадратного уравнения есть некоторая степень пятерки, не превышающая показателя 4. Тогда становится очевидно, что
Переходя от t к x, получаем:
Похожие вопросы
Предмет: Русский язык,
автор: mstfyaltwrh48
Предмет: Английский язык,
автор: ritm11491
Предмет: Қазақ тiлi,
автор: bekturashulmeken
Предмет: Физика,
автор: ната839
Предмет: Математика,
автор: ayanarshabek