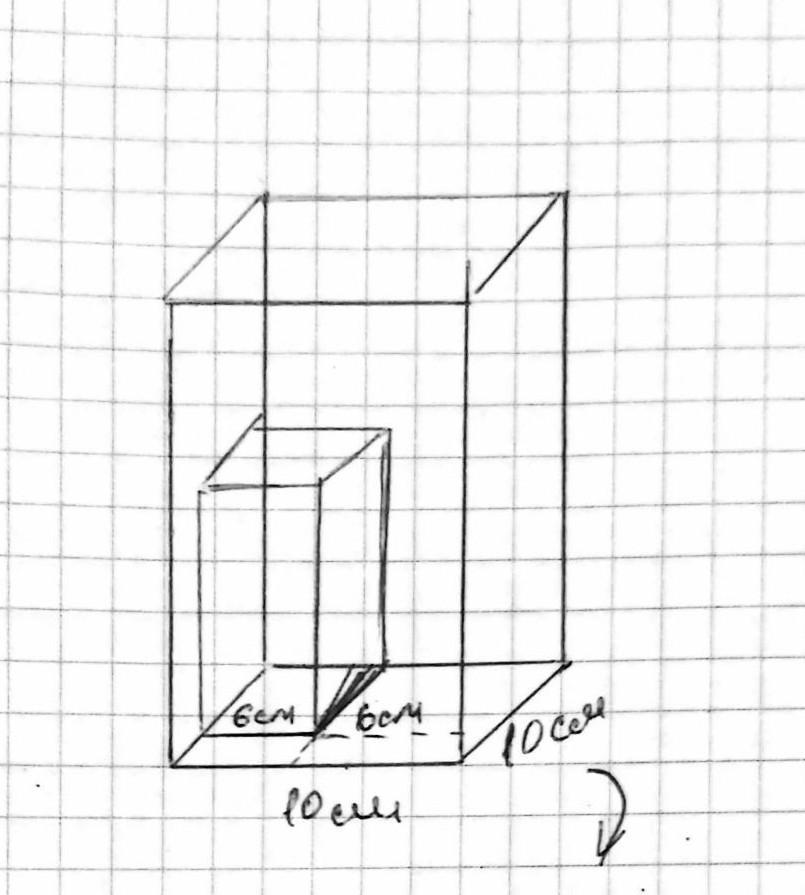
В воду, налитую в сосуд квадратного сечения с вертикальными стенками ( длинна внутренней стороны квадрата 10 см.), опускают с постоянной относительно сосуда скоростью 8 мм/с стакан с квадратным сечением со стороной 6 см. С какой скоростью поднимается вода в сосуде?
Ответы
Ответ:
4,5 мм/с
Объяснение:
Возьмём промежуток времени t = 1 с. За это время стакан опустится в воду на глубину, равную 8 мм (исходя из данной скорости опускания) или 0,8 см.
Тогда стакан вытеснит объем воды, равный собственному объёму, погруженному в воду.
V = 0,8 см × 6 см × 6 см = 28,8 см³
Теперь смотрим приложенную схему. На ней изображён сосуд с погруженным в него стаканом в объеме. Из данной схемы можно сказать: вытесненная вода будет распределяться по свободной от стакана площади S, поднимаясь на некоторую высоту h, которую мы хотим найти.
Искомая площадь S есть ничто иное, как разность площадей большого и малого квадрата, т.е.:
S = (10 см)² - (6 см)² = 100 см² - 36 см² = 64 см²
Если умножить полученную площадь на искомую высоту, получим, очевидно, объем вытесненной воды, полученный раннее (т.к. он весь распределяется по сосуду)
Тогда Sh = V
h = V/S
h = 28,8 см³/64 см² = 0,45 см = 4,5 мм
Возвращаясь к началу задачи, вспоминаем, что на высоту 4,5 мм вода поднимается за 1 секунду. Тогда искомая скорость столбика воды - 4,5 мм/с.