Предмет: Алгебра,
автор: nazariay
Вычислить несобственные интегралы или установить их расходимость
Приложения:
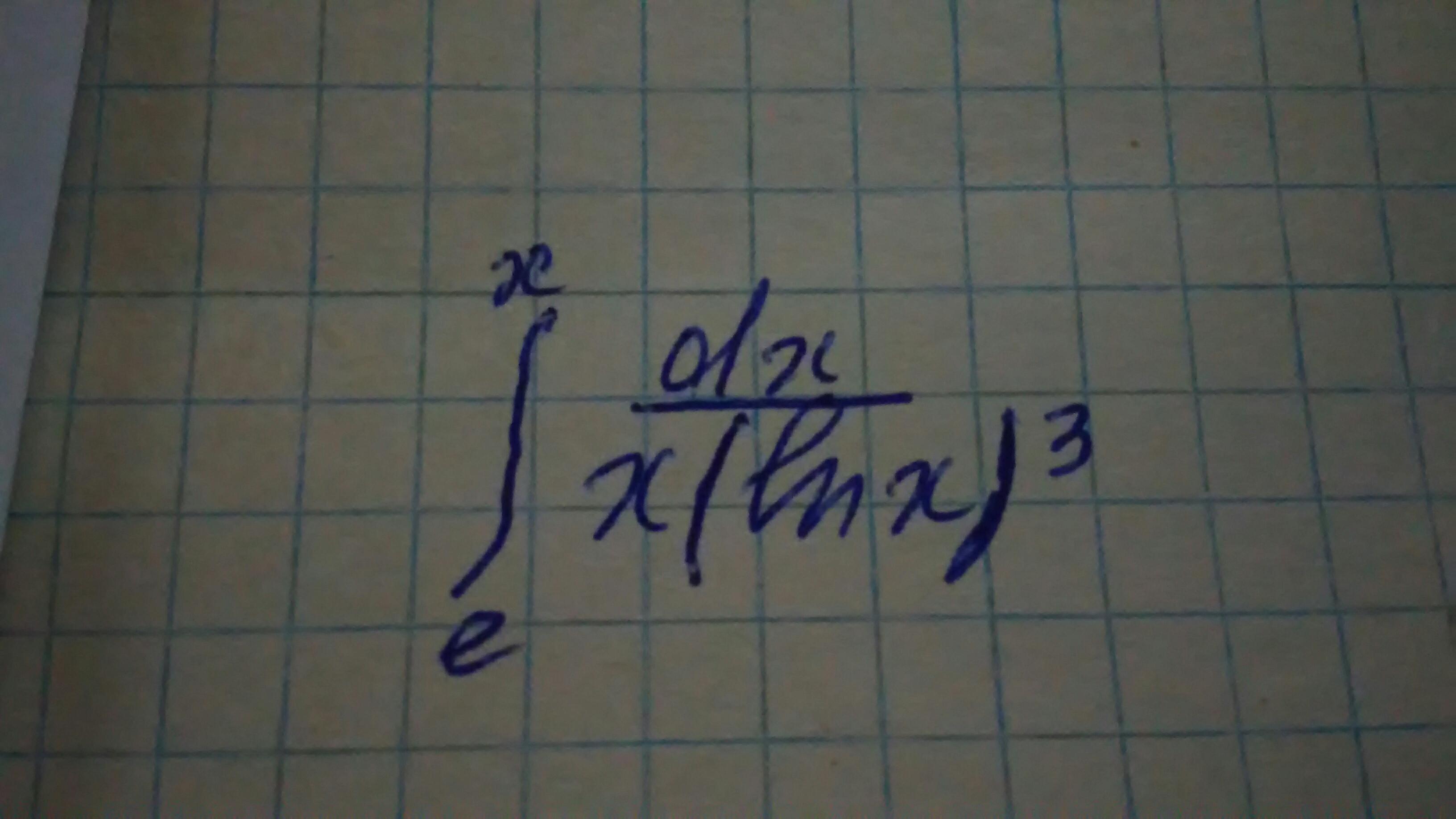
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Подставляя верхние и нижние пределы, получим:
При устремлении x→∞ ln²(x) → ∞, а 1/(ln²(x)) → 0.
Следовательно, данный несобственный интеграл сходится к 1/2.
Автор ответа:
0
Похожие вопросы
Предмет: Другие предметы,
автор: katiailchyshyn
Предмет: Химия,
автор: v9alina
Предмет: Алгебра,
автор: hellingrrr
Предмет: Математика,
автор: тамерлан39
Предмет: История,
автор: Аврамченко