Предмет: Математика,
автор: kdw70
Пожалуйста, помогите
Приложения:

Аноним:
(-1;1)
Ответы
Автор ответа:
1
Найдем корни квадратного уравнения:
Сразу отметим, что если начальное неравенство меньше нуля, при чем перед х² стоит положительный коэффициент (ветви параболы направлены вверх), значит уравнение, которое мы сейчас решаем, должно иметь 2 различных корня!
То есть D>0
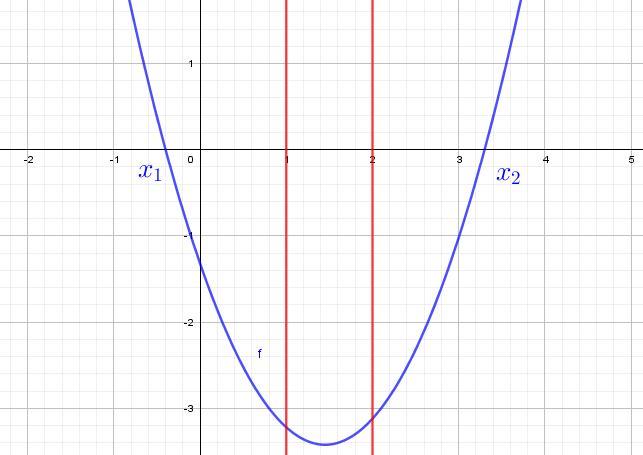
Сделаем схематичный чертеж (см. рисунок)
Из рисунка видно, чтобы парабола была ниже оси Y на отрезке [-1;1], нужно, чтобы ее нули x1 и x2, находились по разные стороны отрезка, то есть:
x1 >2 и х2 <1;
или x1 <1 и x2 >2
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: pastovenskijdaniil
Предмет: Математика,
автор: dnazimovvvv1
Предмет: Русский язык,
автор: varvarapetrova328
Предмет: Математика,
автор: aslanovadiana19
Предмет: Математика,
автор: daryasavkina2