решите неравенство
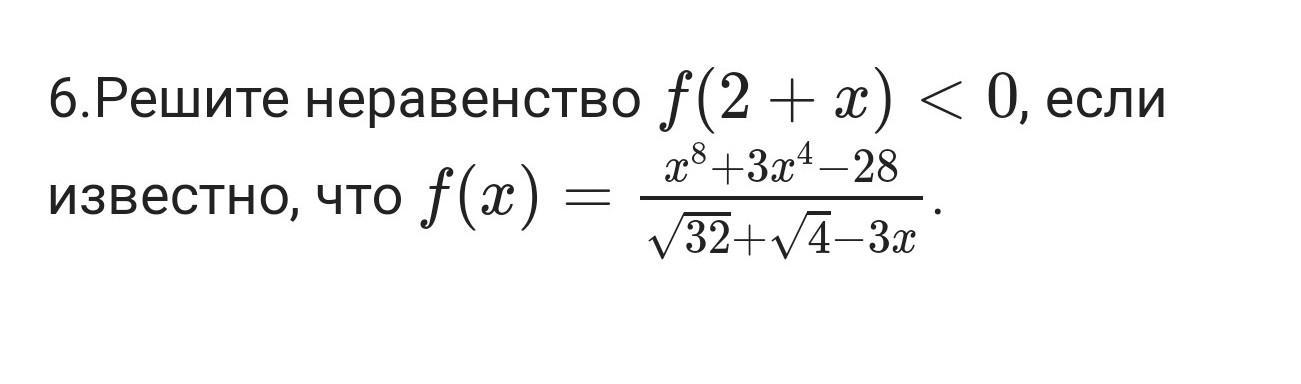
Ответы
f(x) = (x⁸ + 3x⁴ - 28)/(4√2 + 2 - 3x) = (x⁴ + 7)(x⁴ - 4)/(4√2 + 2 - 3x) = (x⁴ + 7)(x² - 2)(x² + 2)/(4√2 + 2 - 3x);
f(2 + x) = ((x + 2)⁴ + 7)((x + 2)² - 2)((x + 2)² + 2)/(4√2 + 2 - 3(2 + x)) = ((x + 2)⁴ + 7)((x + 2)² - 2)((x + 2)² + 2)/(4√2 + 2 - 6 -3x) = ((x + 2)⁴ + 7)((x + 2)² - 2)((x + 2)² + 2)/(4√2 - 4 -3x);
f(2 + x) < 0;
((x + 2)⁴ + 7)((x + 2)² - 2)((x + 2)² + 2)/(4√2 - 4 -3x) < 0;
((x + 2)² - 2)/(4√2 - 4 -3x) < 0;
((x + 2 - √2)(x + 2 + √2))/(4√2 - 4 -3x) < 0;
((x + 2 - √2)(x + 2 + √2))/(4√2 - 4 - 3x) < 0;
x ≠ (4√2 - 4)/3;
((x + 2 - √2)(x + 2 + √2))/(4√2 - 4 - 3x) = 0;
x₁ = -2 + √2; x₂ = -2 - √2
+++++ ------ ++++ -----
---------------------○-------------○-----------○---------------------->
-2 - √2 -2 + √2 (4√2 - 4)/3
x ∈ ( -2 - √2; -2 + √2)U((4√2 - 4)/3; ∞)