Предмет: Математика,
автор: wrestliing98
площадь трапеции равна 36 а основания DC=6, AB=2. на стороне BC взята точка E так что BE=2EC. найти площадь треугольника ADE
antonovm:
21 , если не напутал
Ответы
Автор ответа:
5
Ответ:
21 кв.ед.
Пошаговое объяснение:
В решении использовано следующее утверждение :
Если у 2 треугольников равные высоты , то их площади относятся
как основания , к которым эти высоты проведены
Приложения:
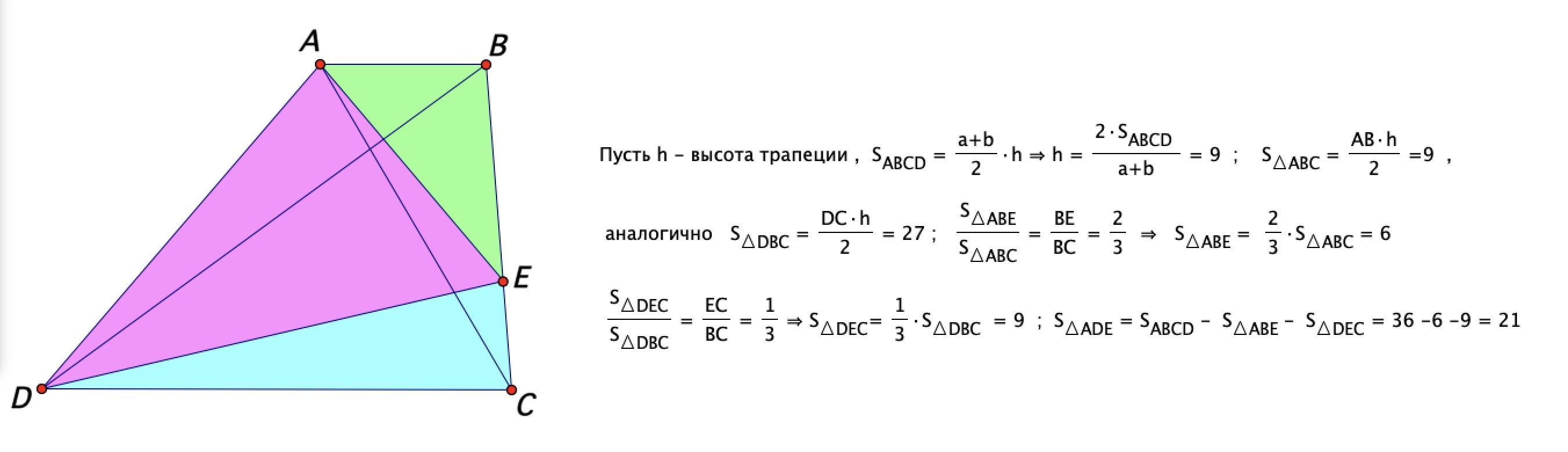
можно чуть проще , щас переделаю
Автор ответа:
5
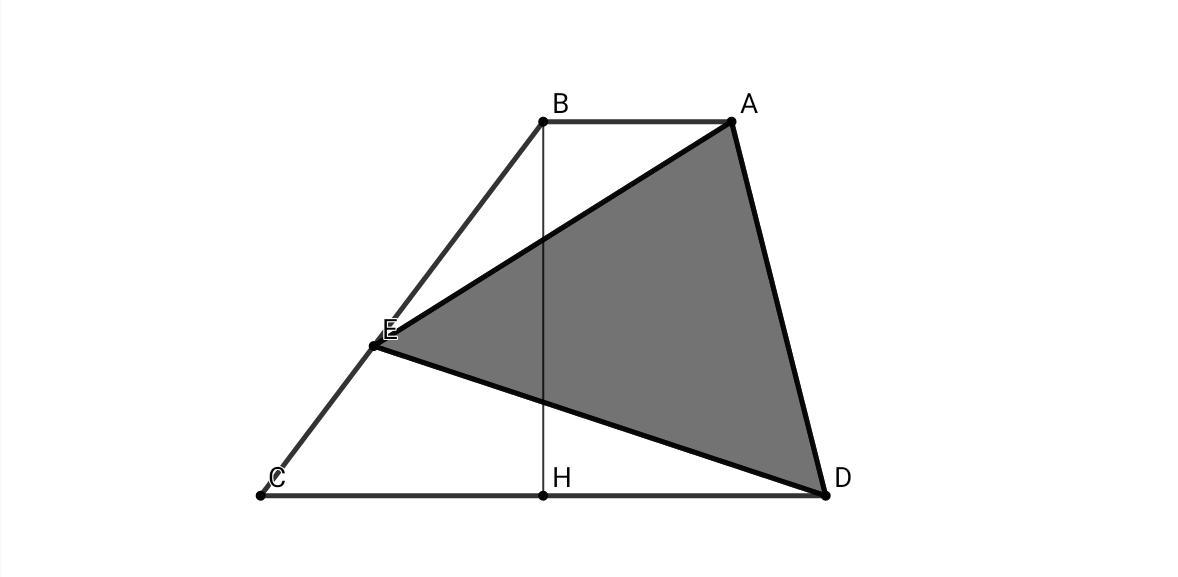
S (abcd) = (AB + CD)•BH/2 = (2 + 6)•BH/2 = 36 ⇒ BH = 9
Пусть СЕ = х , ВЕ = 2х , ∠ВСD = α , ∠ABC = 180° - α
B ΔBCH: sinα = BH/BC ⇒ BH = BC•sinα ; 3x•sinα = 9 ⇒ x•sinα = 3 ; площадь треугольника: S = (1/2)•a•b•sinα
S (ade) = S (abcd) - S (abe) - S (cde) = 36 - (1/2)•2•2x•sinα - (1/2)•6•x•sin(180° - α) = 36 - 5•x•sinα = 36 - 5•3 = 21
ОТВЕТ: 21
Приложения:
Похожие вопросы
Предмет: Химия,
автор: niktohaph
Предмет: Математика,
автор: ksenanazarhyk
Предмет: Математика,
автор: miki818
Предмет: Математика,
автор: арт0873