Question

В равнобедренном треугольнике медиана, проведенная к основанию, равна 16см, а медиана, проведенная к боковой стороне, 2корня97. Вычислите периметр треугольника

Answer 1

Ответ: 64 см

Объяснение:

Answer 2

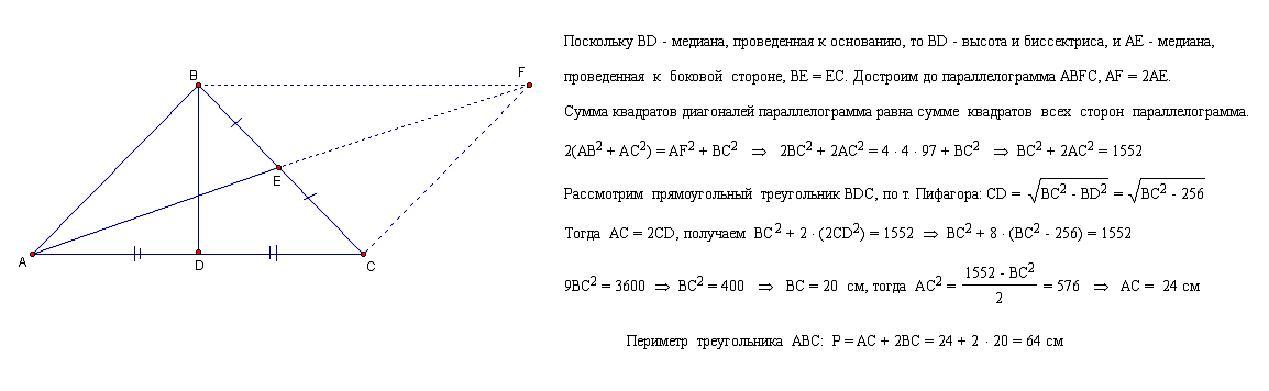
Ответ: Р=20+20+24=64 (см)

Объяснение: медианы точкой пересечения делятся в отношении 2:1, считая от вершины) т.к. медиана к основанию равнобедренного треугольника является и высотой треугольника (и биссектрисой), получим прямоугольный треугольник с катетом 16/3, гипотенузой 4V97/3 и второй катет=половине основания треугольника=

V( (16*97/9)-(16*16/9) ) = V( (16/9)*(97-16) ) = (4/3)*9 = 12

и тогда основание треугольника =24 (см)

из другого прямоугольного треугольника с катетами 16 и 12 можно найти боковую сторону данного треугольника (она будет гипотенузой прямоугольного треугольника); легко заметить, что этот прямоугольный треугольник "египетский" (т.е. его стороны пропорциональны числам 3;4;5):

12=3*4; 16=4*4; гипотенуза будет =5*4=20 (см) и таких стороны две...