Предмет: Математика, автор: MaksMolchDmitr

Вычислите сумму:
$1 + \frac{2}{2} + \frac{3}{ {2}^{2} } + \frac{4}{ {2}^{3} } + ... + \frac{n}{ {2}^{n - 1} }$

DragonetSoul: Интересная задача

Аноним: https://znanija.com/task/32626559 - решение здесь

antonovm: и здесь ( другое)

viva34: долго думал, что ж я не так сделал, что мое решение удалили а это (такое же) оставили. потом понял, что я не до n посчитал, а до бесконечности))

Ответы

Автор ответа: antonovm

Ответ:

Пошаговое объяснение: Решение : /////////////////////

Приложения:

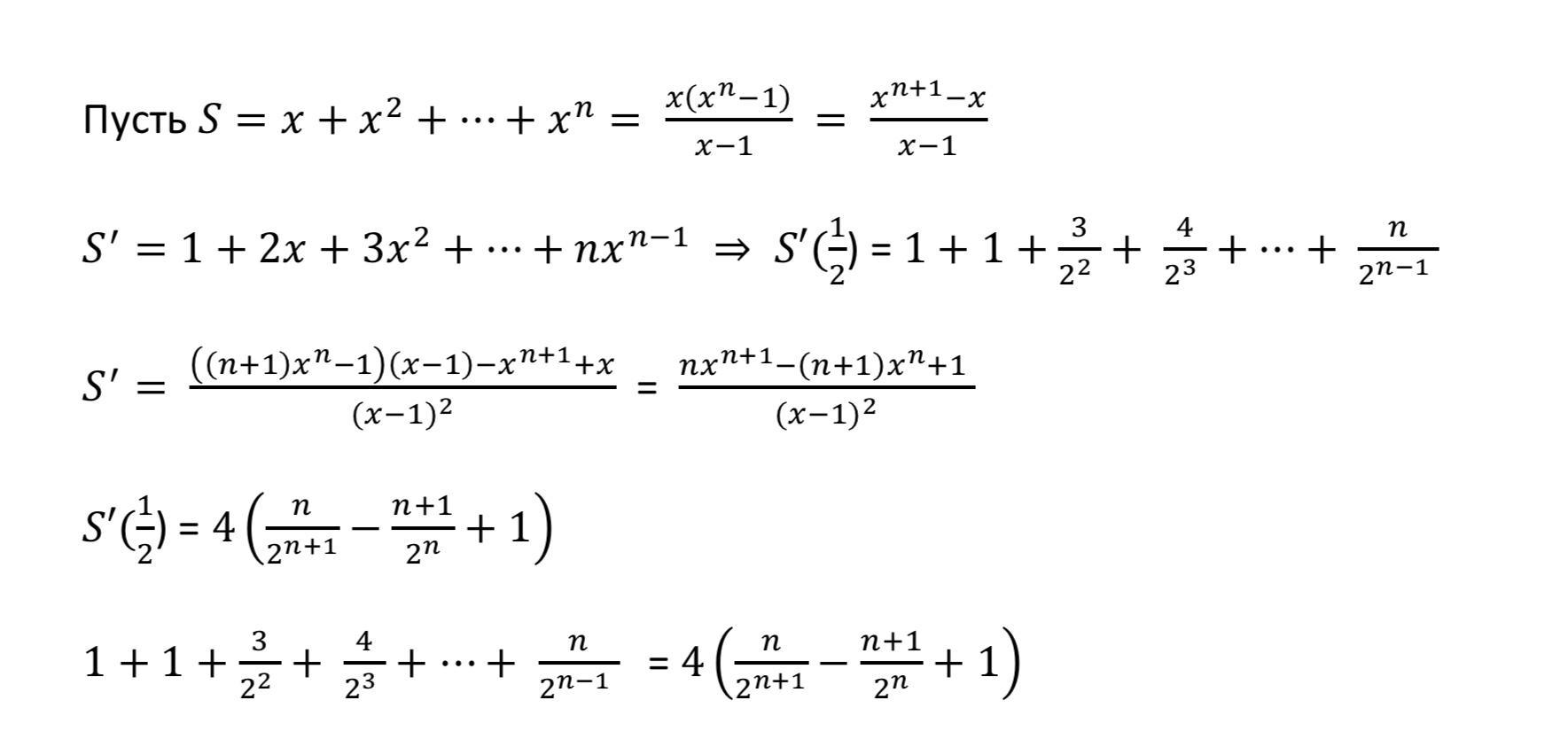
DragonetSoul: а откуда он взялся? как он получился?

MaksMolchDmitr: Грубо говоря от первообразной нашей функции, где за 1/2 мы обозначили x

antonovm: Замените в исходной сумме 1/2 на х , тогда получите : 1 +2x +3x^2 + ...., а это производная от S = x + x^2 +x^3 +... ,значит , если вы найдете производную от S и подставите в нее 1/2 , то вы получите искомую сумму , этот метод часто применяют , если надо суммировать ряд или вычислить матожидание дискретной случайной величины , имеющей бесконечное множество значений

DragonetSoul: не изучал такого метода

antonovm: стандартный метод суммирования числовых рядов , проходят обычно в технических вузах на 2 курсе

DragonetSoul: а предмет мат. анализ? или еще что-то?

DragonetSoul: У нас суммирование по пределу n частичной суммы

antonovm: да , так я и нашел частичную сумму , предел равен 4 ( сумма ряда)

antonovm: Матанализ , 2 курс , но в теории вероятностей ( если вы будете изучать ее основательно ) без этих фокусов не обойтись

DragonetSoul: только вы делали замену какую-то допом

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Алгебра, автор: ShowBest

допоможіть будь ласка