Тележка с передними колёсами диаметром 30 см и задними колёсами диаметром 40 см движется по прямой дороге, проходящей через точки A и B. Между точками А и В ровно 100 метров. Точка А покрашена. Через точку А проезжают правые колёса тележки и в точках соприкосновения с ней эти точки красятся.. В свою очередь, при каждом соприкосновении с дорогой эти точки оставляют свой след в виде точек на дороге. Никакие точки на дороге, кроме точки А, колёса не окрашивают. Тележка движется по направлению от точки А в сторону точки В. Найти:
а) наименьшее расстояние между соседними окрашенными точками
б) количество окрашенных точек на отрезке АВ.
Ответы
Ответ:
Пошаговое объяснение:
Найдем длину каждого колеса
L1=п*d1=3.14*0.3=0.942 м
L2=п*d2=3.14*0.4=1,256 м
а) наименьшее расстояние между соседними окрашенными точками
(4*L1/2 - L2) / 2=(0.942*2 - 1.256)/2=0.314 м =31,4 см
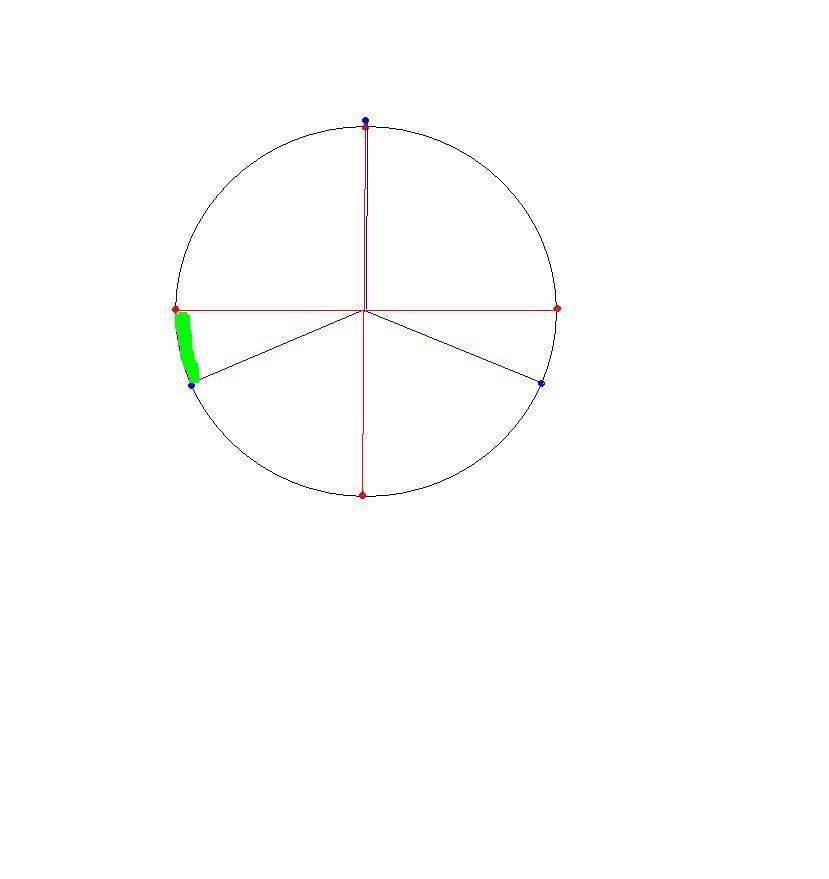
На картинке видно - весь круг - 4 оборота малого колеса или 3 - большого . Нужно найти минимальное расстояние между точками (отмечено зеленым). Следовательно от всей длины круга отнимем половину, затем длину большего колеса (нижний сектор от синей до синей точки). И останется разделить остаток на 2.
б) количество окрашенных точек на отрезке АВ.
N=(S/L1 )+ (S/L2) =106 + 79 =185 точек
Здесь: S/L - количество длин окружностей каждого колеса укладывается в расстояние между АВ без остатка.
Но у нас совпадают каждая 4 точка малого колеса с большой.
Тогда
Nob=N - (S/L1 ) /4 =185 - (106/4 - 1)=185 - 25= 160 штук