Предмет: Математика,
автор: seregauglov
решите неравенство
НУЖНО ПОЛНОЕ РЕШЕНИЕ И ОТВЕТ!
Приложения:
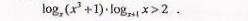
Ответы
Автор ответа:
2
Исходное неравенство равносильно системе:
Ответ: (2; +∞).
Приложения:

Похожие вопросы
Предмет: Информатика,
автор: Rokleen
Предмет: Математика,
автор: lerachkawxsf
Предмет: Другие предметы,
автор: zxzccxzvcxvb
Предмет: Математика,
автор: хорошистик6
Предмет: Химия,
автор: Аноним