Question

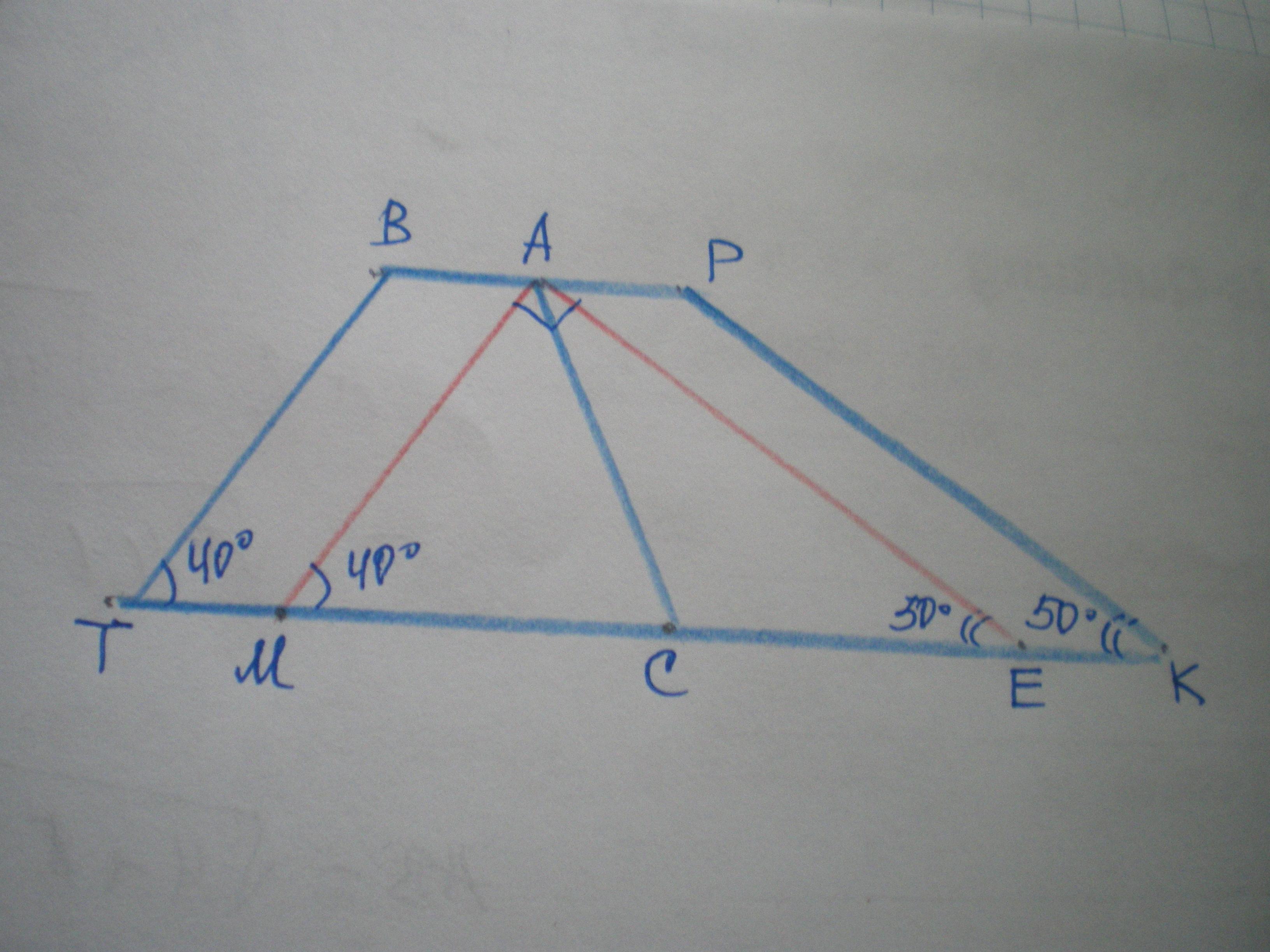
Основания трапеции равны 16 см и 10 см. Углы при большем основании равны 40 и 50 градусов. Найдите длину отрезка, соединяющего середины оснований.
Подробно, пожалуйста.

Answer 1

Ответ:

13 см.

Объяснение:

Дано: ТВРК - трапеция, ∠Т=40°, ∠К=50°, АВ=АР, ТС=СК, ВР=10 см, ТК=16 см.

Найти АС.

Если сумма углов в трапеции при основании равна 90 градусов, то длина отрезка, соединяющего середины оснований , равна половине разности длин оснований.

Докажем это.

Проведем АМ║ВТ и АЕ║РК

∠Т+∠К=40+50=90°, значит АС=1/2(ТК-ВР)=1/2(16-10)=1/2 * 6 = 3 см.

АВТМ - параллелограмм по построению, ВА=ТМ.

АЕКР - параллелограмм по построению, АР=ЕК.

По условию АВ=АР=1/2 ВР, значит, АВ=АР=ТМ=ЕК=1/2ВР.

ТК=ТМ+МС+СЕ+ЕК

МЕ=ТК-(ТМ+ЕК)

ТМ=ЕК=1/2ВР

МЕ=ТК-(ТМ+ЕК)=ТК-(1/2ВР+1/2ВР)=ТК-ВР

Рассмотрим ΔАЕМ. ∠АЕМ=∠РКТ как соответственные углы при ВР║ТК и секущей АС.

т.к. ∠ВТК+∠РКТ=40+50=90°, то и ∠АМЕ+∠АЕМ=90°

а т.к. сумма углов треугольника составляет 180°, то ∠МАЕ=180-90=90°, т.е. ΔМАЕ - прямоугольный

По условию ТС=СК, по построению ТС=ТМ+МС, СК+СЕ+ЕК, следовательно ТМ+МС=СЕ+ЕК.

Но ТМ=ЕК, значит МС=СЕ.

По определению медианы треугольника АС - медиана, выходящая из прямого угла. По свойству медианы, проведенной к гипотенузе, АС=1/2МЕ.

МЕ=ТК-ВР

Подставим это значение в формулу для АС

АС=(ТК-ВР)/2=1/2(16-10)=1/2 * 6 = 3 см.

Ответ: 3 см.