Предмет: Геометрия, автор: wihines

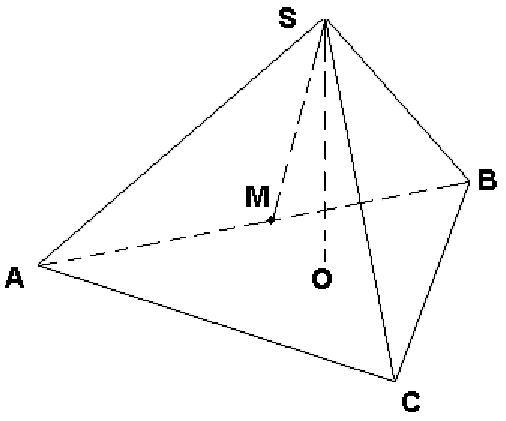
В правильной треугольной пирамиде SABC
M- середина ребра AB
S- вершина
BC = 4
Sбок = 174
Найти SM

Аноним: 29

Ответы

Автор ответа: Аноним

0

Поскольку все грани правильной треугольной пирамиды это равнобедренный треугольник и точка М - середина АВ, то

SM - медиана, высота и биссектриса равнобедренного треугольника SAB.

Площадь боковой поверхности пирамиды вычисляется по формуле

$S_{bok}=\dfrac{1}{2}P_o\cdot h$

где Ро - периметр основания, h - апофема(в нашем случае это SM)

$SM=\dfrac{2S_{bok}}{P_o}=\dfrac{2\cdot 174}{3\cdot 4}=29$

Приложения:

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: География, автор: belovamariyaa

2. Охарактеризуйте зростаючий тип статево-вікової піраміди. Яким країнам він характерний?

6 лет назад

Предмет: Математика, автор: tanyashulunova89

Найдите один неправильный ответ, а в случае его отсутствия

укажите: «Неправильного ответа нет».

А 1. Существенными признаками понятия «арифметическая задача» является наличие в тексте:

1) условия; 2) вопроса; 3) числовых данных;

4) реального сюжета; 5) взаимосвязи между условием и вопросом;

6) неправильного ответа нет.

А 2. В начальном обучении арифметические задачи выполняют следующие функции:

1) развитие разных видов мышления;

2) ознакомление с некоторыми математическими понятиями и закономерностями;

3) подготовка к жизни, в том числе к продолжению образования;

4) заучивание способов решения типовых задач;

5) воспитание некоторых качеств личности;

6) неправильного ответа нет.

А 3. На этапе ознакомления с арифметической задачей и ее структурой тексты задач полезно сравнивать с:

1) загадками;

2) короткими рассказами, где встречаются имена числительные или слово «сколько»;

3) математическими рассказами, где некоторая ситуация полностью описана на математическом языке;

4) задачами-шутками;

5) другими арифметическими задачами;

6) неправильного ответа нет.

А 4. Решить арифметическую задачу – это значит:

1) объяснить, какие действия и почему надо выполнить, чтобы найти требуемое в задаче;

2) вычислить;

3) сопоставить смысл полученного числа с требованием задачи;

4) проверить вычисления; 5) ответить на вопрос задачи;

6) неправильного ответа нет.

А 5. Решение любой арифметической задачи ведется по одному и тому же плану:

1) подготовительная работа;

2) восприятие и осмысление содержания задачи;

3) поиск и составление плана решения;

4) выполнение решения и ответ на вопрос задачи;

5) проверка;

6) работа над решенной задачей (творческая работа).

А 6. Обучение решению задач осуществляется поэтапно:

1) подготовительная работа;

2) работа по разъяснению текста задачи;

3) «открытие» арифметического способа решения задачи;

4) «взгляд назад» или рефлексия;

5) закрепление, т. е. формирование умения применять тот же способ в аналогичных задачах;

6) неправильного ответа нет.

А 7. В начальных классах арифметические задачи решаются следующими способами:

1) практическим; 2) арифметическим; 3) геометрическим;

4) алгебраическим; 5) подбора; 6) неправильного ответа нет.

А 8. Чтобы организовать на уроке решение задачи практическим способом, можно использовать:

1) полное иллюстрирование текста;

2) условно-предметное моделирование;

3) графическое моделирование;

4) краткую запись задачи;

5) неправильного ответа нет.

А 9. Чтобы «открыть» вместе с детьми арифметический способ решения задачи, можно:

1) полностью отказаться от наглядной интерпретации задачи;

2) проиллюстрировать только сюжет;

3) записать задачу кратко;

4) использовать предметное моделирование лишь части условия;

5) выполнить полное предметное моделирование текста задачи;

6) неправильного ответа нет.

А 10. В процессе обучения решению простых задач у учащихся формируются следующие общие умения:

1) выразительно читать; 2) выделять условие и вопрос;

3) обоснованно выбирать арифметическое действие, соответствующее описанной в тексте взаимосвязи между данными и искомым;

4) использовать для выбора арифметического действия и обоснования его правильности различные виды моделей;

5) оформлять запись решения; 6) применять способы проверки.

6 лет назад

Предмет: Английский язык, автор: faizulinmarat403

Помогите пожалуйста пж

6 лет назад

Предмет: Литература, автор: inderbievaaidka

каким было 1 свидание онегина и татьяны?

9 лет назад

Предмет: География, автор: maxtayfunow201

каковы закономерности расположения гор и обширных равнин на поверхности Земли и как это проявляется на материках Южного полушария

9 лет назад