Предмет: Алгебра,
автор: elvirasalavatova
Помогите , пожалуйста, решить
Приложения:
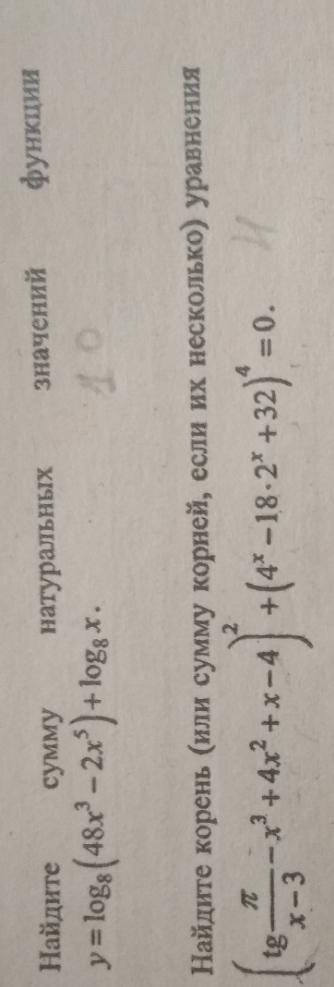
Ответы
Автор ответа:
2
1
Ф-ция при таких принимает натуральные значения от
Ответ: 10
2
Подставим корни 2-ого выражения в первый.
корень
тангенс для аргумента не определён
не корень
Ответ: 4
elvirasalavatova:
Спасибо большое:)
Похожие вопросы
Предмет: Математика,
автор: karagulovamalika39
Предмет: Математика,
автор: leyla0607
Предмет: Українська мова,
автор: nikolyastremskaya
Предмет: Математика,
автор: qbcd
Предмет: Алгебра,
автор: tima170