Предмет: Математика,
автор: vladosziablits
Ребят, очень нужна помощь!!!!!! Даю почти 25 балов
Приложения:
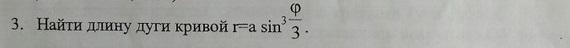
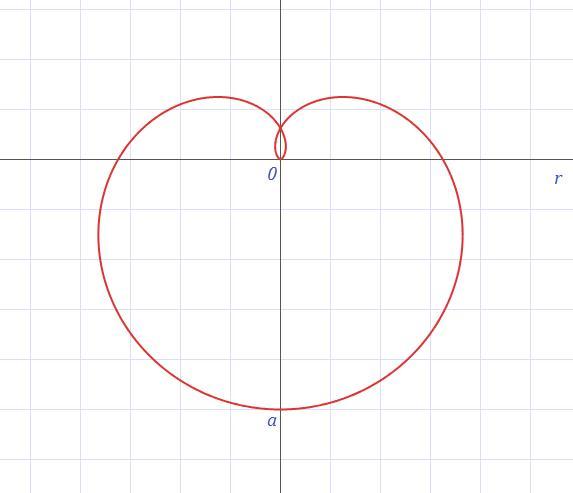
Ответы
Автор ответа:
1
Приложения:
Похожие вопросы
Предмет: Физика,
автор: sofiya2020v
Предмет: Русский язык,
автор: nekarmaksim
Предмет: Математика,
автор: Hychtopisat
Предмет: Математика,
автор: 6417257
Предмет: Математика,
автор: ангелинаМ11