Предмет: Алгебра,
автор: мудрейшая2401
Решите уравнение с подробным решением.
Приложения:
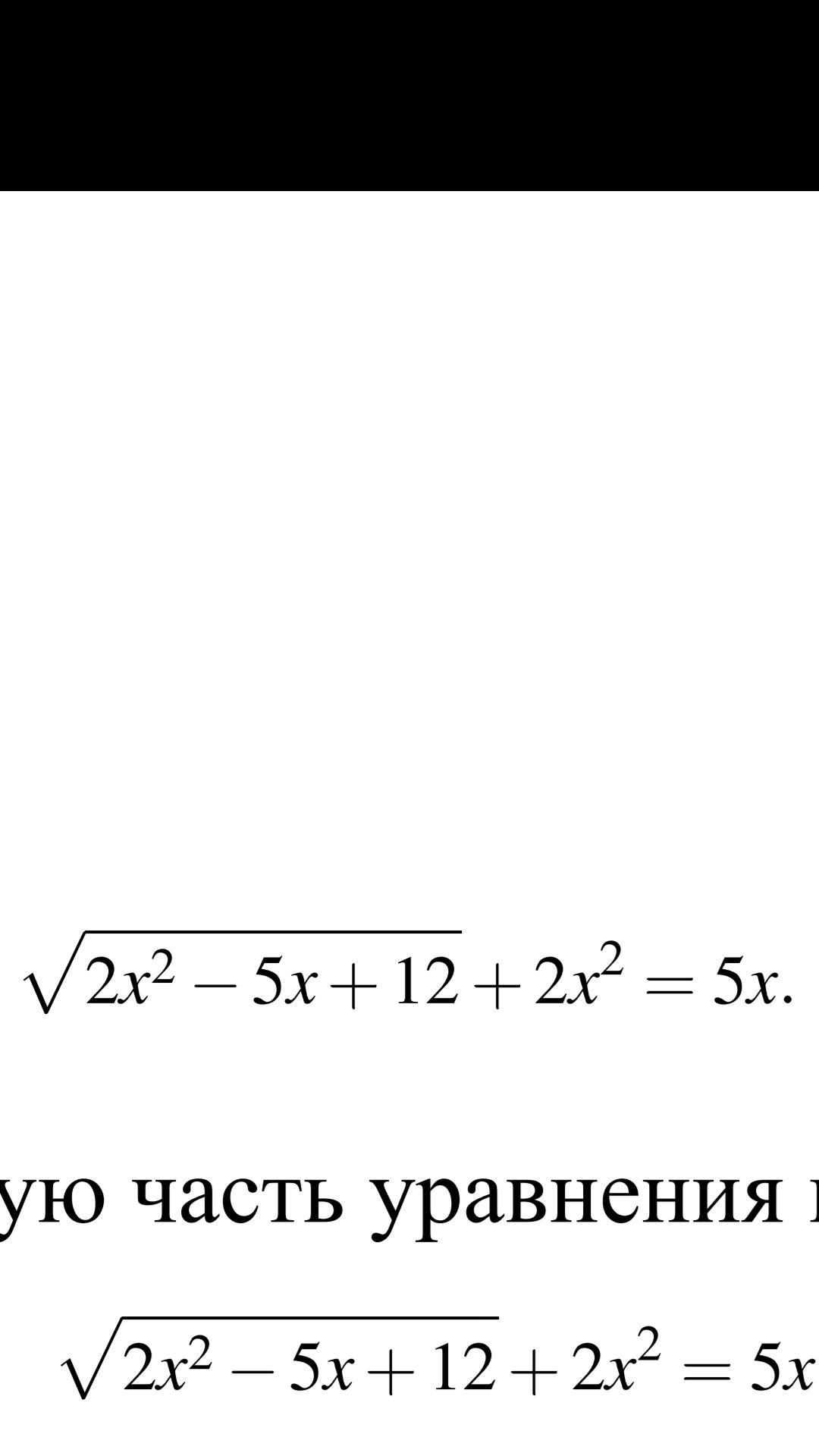
Ответы
Автор ответа:
2
Пусть
Уравнение имеет корни 2 и 3, значит, исходное уравнение имеет корни
и
.
Ответ: 1; 1,5
Автор ответа:
1
Решение во вложении. Удачи в учёбе,мой друг!
P.S. Выражение с корнями не подходит, так как вычисляется приближенное значение.
Приложения:

DNHelper:
И что, что приближённое значение? Это ничего не объясняет. Раз корни откуда-то вышли, их тоже нужно проверить. А так я тоже могу через Photomath прогнать уравнение и, не думая, переписать.
мне не составит труда их проверить, но это не разумно в данном случае
В смысле неразумно? А вдруг они подошли бы? Вы же не знаете наверняка.
Похожие вопросы
Предмет: Українська мова,
автор: natia3999com
Предмет: Литература,
автор: youxde
Предмет: Алгебра,
автор: daun2w313123
Предмет: Литература,
автор: Лулс