Предмет: Алгебра,
автор: sashabaster
Готовлюсь к Экзамену, совсем забыл как решать тригонометрические уравнения. Что делать со скобками? Объясните порядок решения.
Приложения:
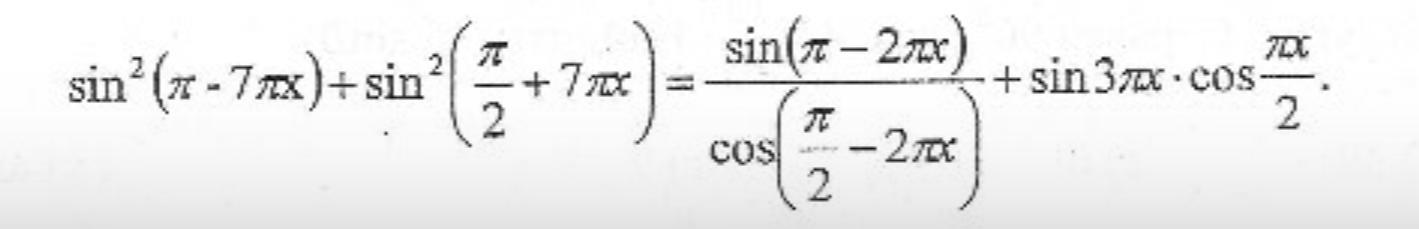
LFP:
именно эти скобки можно "убрать", применив формулы приведения) например, sin(pi-7pi*x)=sin(7pi*x)
sin(pi/2+7pi*x)=cos(7pi*x)
Ответы
Автор ответа:
10
Ответ:
решение представлено на фото
Приложения:


в уравнении есть ограничения (ОДЗ указывать нужно)...
например, х не может быть =2) т.е. n≠6...
да, сейчас
у меня получается x не равен n/2
Автор ответа:
14
Ответ:
x = k/3; k € Z
Объяснение:
Область определения
cos(П/2 - 2Пх) ≠ 0
П/2 - 2Пх ≠ П/2 + Пm; m € Z
x ≠ - m/2; m € Z
Формулы приведения.
sin(П - 7Пх) = sin(7Пх)
sin(П/2 + 7Пх) = cos(7Пх)
sin(П - 2Пх) = sin(2Пх)
cos(П/2 - 2Пх) = sin(2Пх)
Подставляем.
sin^2(7Пх) + cos^2(7Пх) = sin(2Пх) / sin(2Пх) + sin(3Пx)*cos(Пх/2)
1 = 1 + sin(3Пх)*cos(Пх/2)
sin(3Пх)*cos(Пх/2) = 0
Если произведение равно 0, то один из множителей равен 0.
1) sin(3Пх) = 0
3Пх = П*k; k € Z
x1 = k/3; k € Z - это решение.
2) cos(Пх/2) = 0
Пх/2 = П/2 + П*n; n € Z
x2 = 1 + 2n; n € Z
x ≠ - m/2; m € Z
Но при любом n можно подобрать такое m, что будет
x2 = 1 + 2n = - m/2
Поэтому никакое х2 не подходит по области определения.
сложно
А кому сейчас легко?
Похожие вопросы
Предмет: Химия,
автор: sixmelnik
Предмет: Українська мова,
автор: hija19
Предмет: Математика,
автор: clashminikika
Предмет: Математика,
автор: tomilolga