Помогите решить неравенство
Буду благодарна
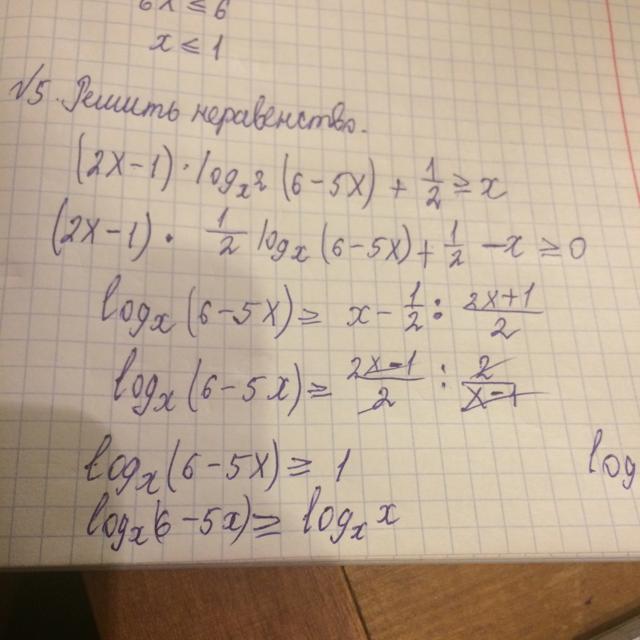
Ответы
Ответ:
Я так понимаю, решить его с самого начала)
(2x-1)log(x^2) (6-5x) + 1/2 >= x
(x-1/2) * log |x| (6-5x) - (x-1/2)>=0 !!! Тут в основании модуль х - |x| !!!
(x-0.5)(log |x| (6-5x) -1 ) >=0
(x-0.5) ( |x| - 1 ) ( 6 - 5x - |x| ) >=0
В строчке выше был применен метод рациональзации вида:
log (a) (f(x)) - log (a) (g(x)) >=0 равносильно с учетом области определения
(a-1)(f(x) - g(x)) >= 0
Далее решаем :)
Рассмотрим два случая: когда x<0 и когда x>=0, так как на этим промежутках модули раскрываются с разными знаками. Рассмотрим первый, когда x отрицателен, т. е. < 0. Тогда |x| = -x. Подставим это в неравенство:
(x - 0.5) ( -x - 1 ) (6 - 5x - (-x)) >=0
( x - 0.5) (x + 1 ) ( 4x - 6) >=0 !!! Тут мы разделили на -1 дважды, поэтому знак неравенства не изменился. !!!
Далее применим метод интервалов, не забывая о том, что x < 0
Решение данного неравенства: x = [-1; 0)
Аналогично рассмотрим случай, когда x >=0. Тогда |x| = x. Подставим это в неравенство.
(x-0.5)(x-1)(6-5x-x)>=0
(x-0.5)(x-1)(x-1)<=0 !!! Тут у нас корень четной кратности, а так же мы разделили на -6 обе части, поэтому изменили знак неравенства !!!
Применим снова метод интервалов, не забывая, что x >=0 :)
x = [0, 1/2] и x = {1}.
А теперь настало время найти область определения нашего неравенства. Подлогарифмическое выражение строго больше нуля, а основание больше нуля и не равно единице. Что же, запишем это математическим языком.
x^2 > 0 => x - любое.
x^2 "не" = 1 => x "не"= "плюс-минус" 1.
6 - 5x > 0 => x < 1.2
Теперь, пересекая все полученные множества, можем записать ответ.
x = (-1; 0.5]
Ответ: x = (-1; 0.5]
(
Объяснение:
Надо было поподробнее