Предмет: Математика,
автор: Davronchis
Исследуйте ряд на сходимость (если что "n+1" в скобках)
Приложения:
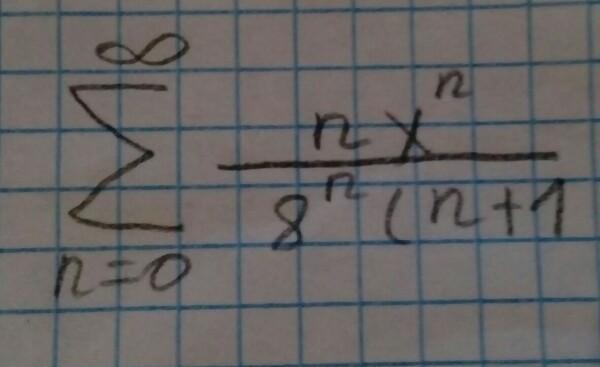
Ответы
Автор ответа:
1
Ответ:
область сходимости
Пошаговое объяснение:
- функциональный степенной ряд
Пусть , Пусть
Найдём предел:
Пусть
- знакоположительный ряд
- ряд расходится по достаточному признаку расходимости, т.к. предел равен 1
Пусть
- знакочередующийся ряд.ряд расходится по достаточному признаку расходимости, т.к. предел равен 1
Ответ: область сходимости
DragonetSoul:
Сейчас дорешаю, а то плохо видно
Похожие вопросы
Предмет: Алгебра,
автор: bogdana14992
Предмет: Физика,
автор: nazarbabij26
Предмет: Математика,
автор: evagrig18072011
Предмет: Математика,
автор: ovrashko67