Предмет: Геометрия,
автор: Leman389
Найти точку пересечения двух взаимно перпендикулярных прямых, проходящих через фокусы гиперболы  , если известно, что точка А(1, 12) лежит на прямой, проходящей через левый фокус с гиперболы.
, если известно, что точка А(1, 12) лежит на прямой, проходящей через левый фокус с гиперболы.
Ответы
Автор ответа:
2
Фокусное расстояние гиперболы c = √(a² + b²) = √(16 + 9) = 5.
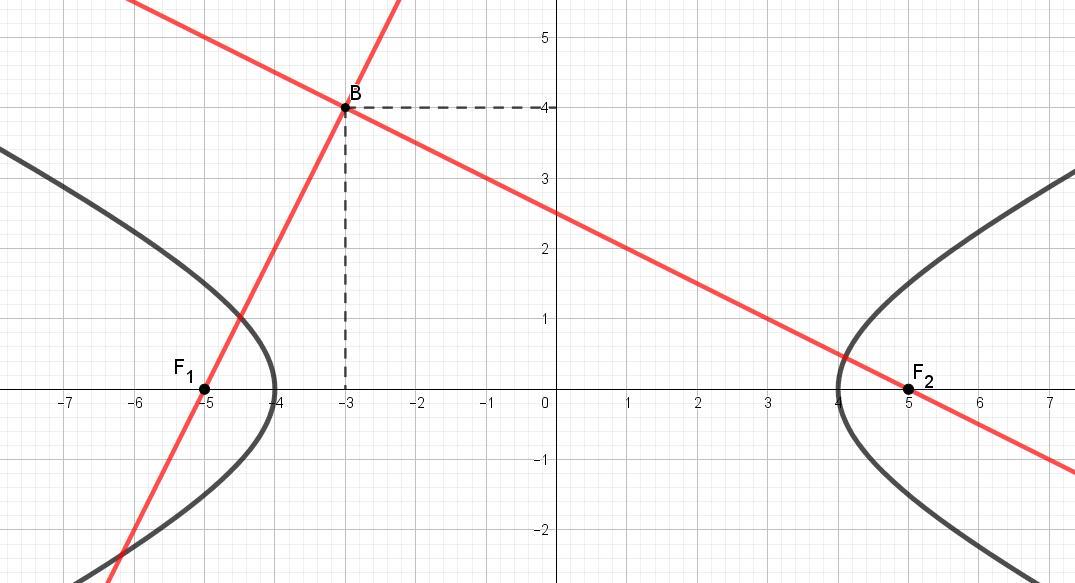
Координаты фокусов F1(-5; 0) и F2(5;0).
Уравнение прямой, проходящей через точки F1 и А(1; 12):
(x + 5)/6 = y/12, сократив на 6, получаем у = 2х + 10.
Перпендикулярная прямая имеет угловой коэффициент к2 = -1/к1 = -1/2. Уравнение её у = (-1/2)х + в. Для определения параметра в подставим координаты точки F2, через которую должна пройти прямая. 0 = (-1/2)*5 + в, отсюда в = 5/2 = 2,5.
Уравнение у = (-1/2)х + 2,5.
Точку пересечения двух взаимно перпендикулярных прямых, проходящих через фокусы гиперболы, находим, приравняв уравнения.
2х + 10 = (-1/2)х + 2,5. Умножим на 2:
4х + 20 = -х + 5. 5х = -15 х = 15/3 = -3. у = 2*(-3) + 10 = -6 + 10 = 4.
Ответ: (-3; 4).
Приложения:
Похожие вопросы
Предмет: История,
автор: asirenko53
Предмет: Математика,
автор: ofantonina1982
Предмет: Литература,
автор: radaakmatova14
Предмет: Литература,
автор: умники9
Предмет: Математика,
автор: marichamaricha