Предмет: Геометрия,
автор: Damboldorn
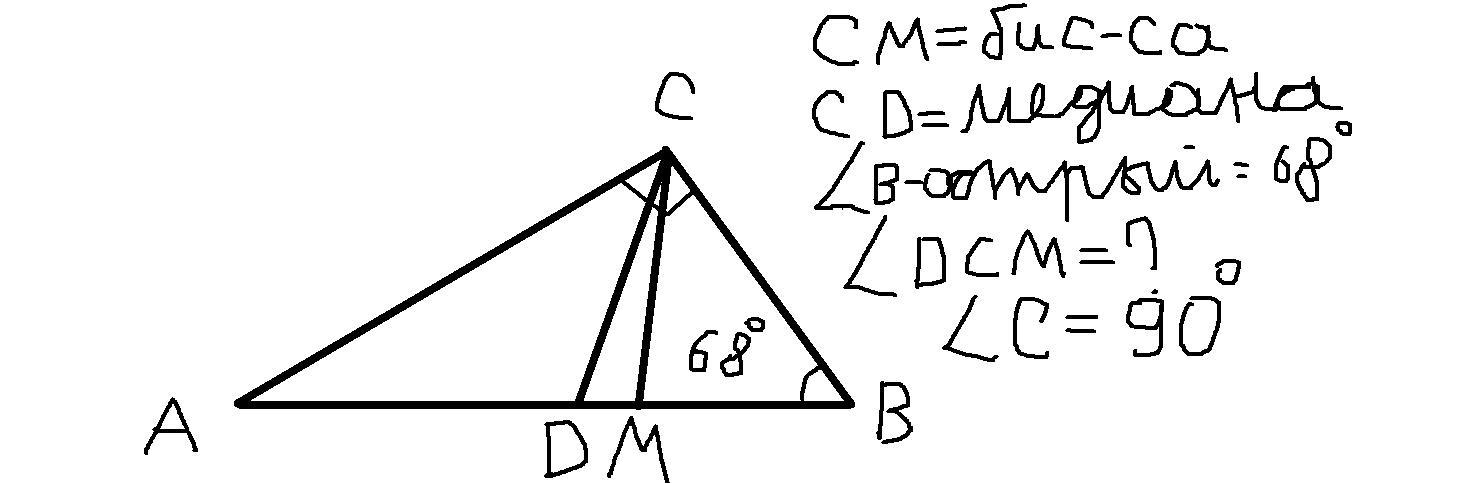
В треугольнике ABC CM-биссектриса, острый угол B=68, CD=медиана, угол C=90
Найдите угол между медианой и бииссектрисой (угол DCM)
Приложения:
Ответы
Автор ответа:
0
Ответ:
решение представлено на фото
Приложения:

Автор ответа:
1
∠САВ=180°-90°-68°=22°, Т.к. СД-медиана ΔАВС, и угол С - прямой, то она равна половине гипотенузы АВ, т.е. ΔАСД- равнобедренный, углы при основании АС равны, ∠АСД=∠ДАС=∠САВ=22°
Т.к. СМ-биссектриса, то ∠МСА=90°/2=45°, тогда искомый
∠ДСМ=∠МСА-∠АСД=45°-22°=23°
Ответ 23°
Похожие вопросы
Предмет: Русский язык,
автор: abraevaaisha2509
Предмет: Другие предметы,
автор: DashaDdd123
Предмет: Математика,
автор: darennna6340
Предмет: Математика,
автор: endgemingaleev