Найт предел функции
Ответ будет -2/9, но не знаю, как его получить, нужно подробное решение
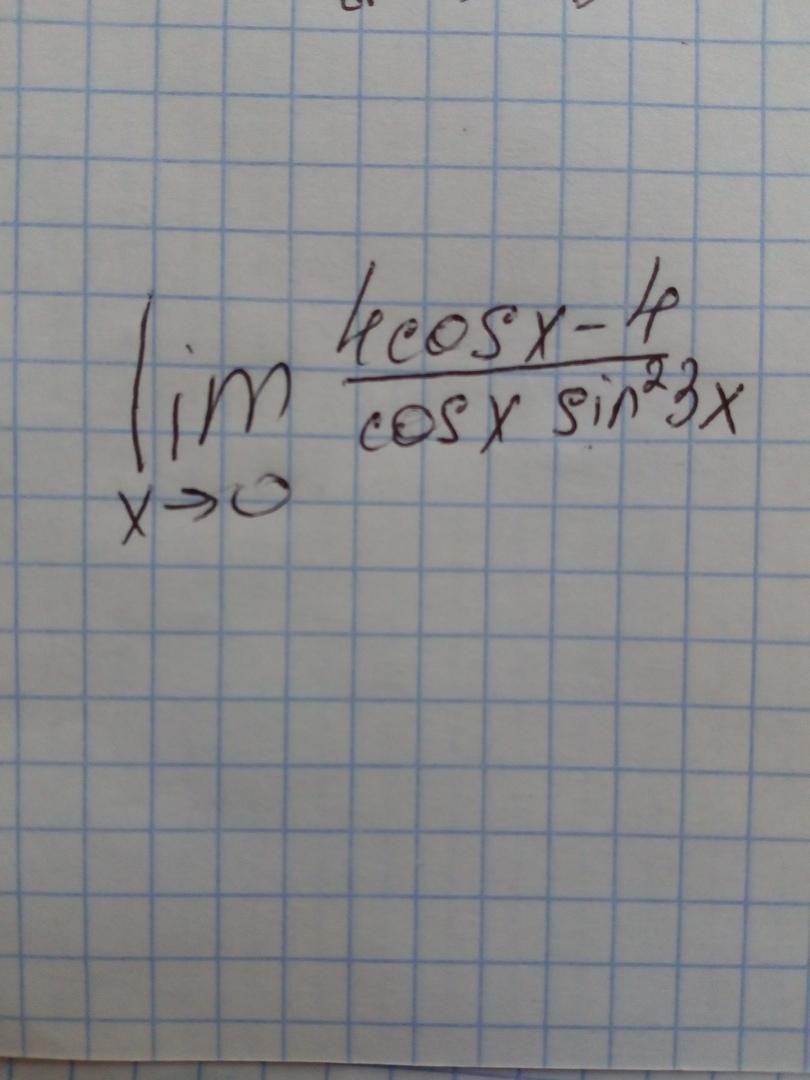
Ответы
Имеем неопределенность 0/0, пределы от числителя и знаменателя при указанном стремлении к нулю икса существуют. Есть смысл пролопиталить. Найдем производные от числителя и знаменателя и разделим производную числителя на производную знаменателя.
-4sinx/(-sinx*sin²3x+2*3cosxsin3x*cos3x)=
-4sinx/(-sinx*sin²3x+3cosxsin6x)
При решении пользовался формулой синуса двойного аргумента sin2x=2sinx*cosx.
ОТ неопределенности не избавились. Еще раз найдем производные числителя и знаменателя, поделим производную числителя на производную знаменателя, получим
(-4cosx)/(-cosx*sin²3x-3*2*sinx*sin3x*cos3x-3sinx*sin6x+3*6cosx*cos6x)
Подставляем вместо х нуль. Все слагаемые, содержащие синус, уничтожатся, т.к. синус нуля равен нулю. Останется -4*cos0/18cos0*cos(6*0)=-4/18=-2/9.
Ответ, как Вы и ожидали, -2/9
Ответ:
=-2/9
Пошаговое объяснение:
=lim(x->0) (-8sin^2x/2)/cosxsin^2(3x)=
=lim(x->0) (-8sinx/2sinx/2*3x*3x*x^2*(1/4)/(cosx*sin3x*sin3x*(x/2)*(x/2)* (9x^2))=
=lim(x->0) (-8*1/4*x^2)/(cosx*9*x^2)=lim(x->0) -2/9cosx=-2/9
использован первый замечательный предел
lim(x->0) sinx/x=1
cosx-1=-2sin^2x/2