Question

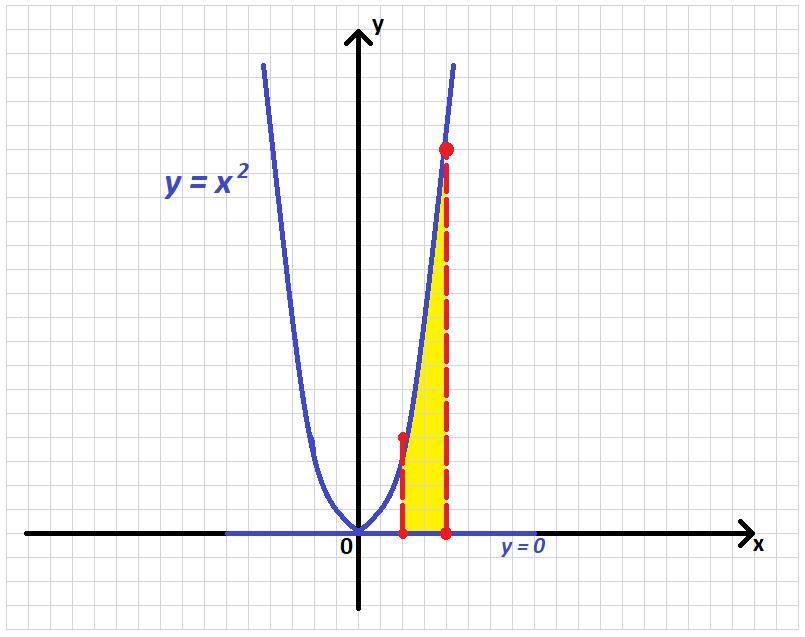
вычислить предварительно сделав рисунок площадь фигуры ограниченной линиями :y=x^2, y=0, x=2, x=4

Answer 1

Найти площадь фигуры, ограниченной кривыми.

Для решения задачи в первую очередь нужно построить график.

По графику видно, что найти нужно площадь области, лежащей над $\bf y = 0$ и под $\bf y = x^2$.

Также из графика получаем, что прямая $\bf x = 2$ будет являться границей фигуры слева, а прямая $\bf x = 4$ — справа.

Найти площадь фигуры, ограниченной сверху графиком функции $\bf y = x^2$, а снизу функцией $\bf y = 0$, а так же прямыми $\bf x = 2$ и $\bf x = 4$ по оси Х, значит вычислить следующий определённый интеграл.

$\int\limits_2^4x^2dx = \dfrac{x^3}{3}\Big|_2^4 = \dfrac{4^3 - 2^3}{3} = \dfrac{64 - 8}{3} = \dfrac{56}{3} = 18\dfrac{2}{3} = 18,(6).$

Ответ: $\bf18\dfrac{2}{3} = 18,(6)$.