Предмет: Математика,
автор: xFuuuuuuuury
Найти дифференциалы первого и второго порядков:
Приложения:
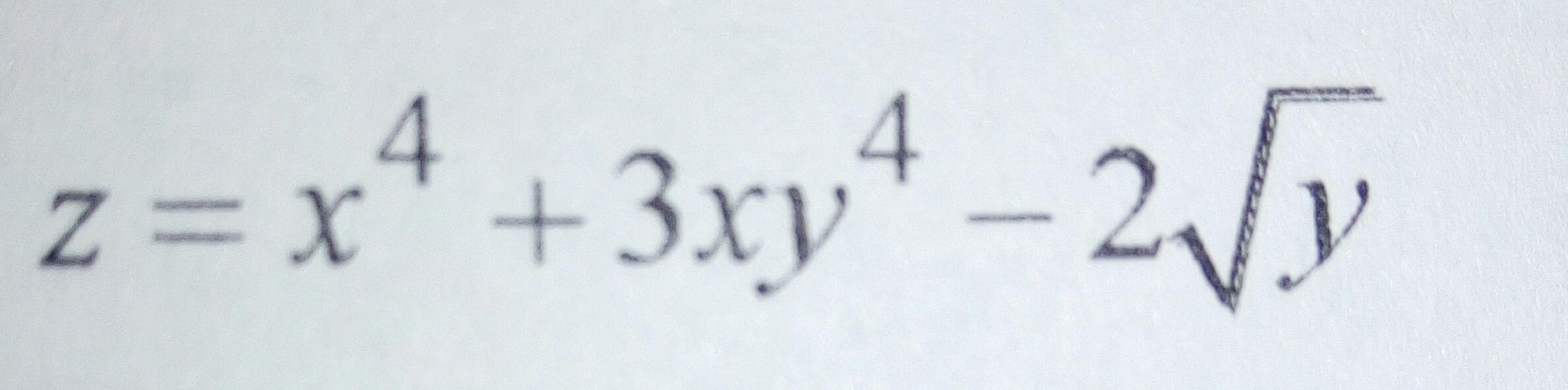
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Физика,
автор: ulyaods
Предмет: Українська мова,
автор: martinukola3
Предмет: Українська література,
автор: vigovskaiao
Предмет: Биология,
автор: alisaglazkova
Предмет: Математика,
автор: OlesyaSk7541