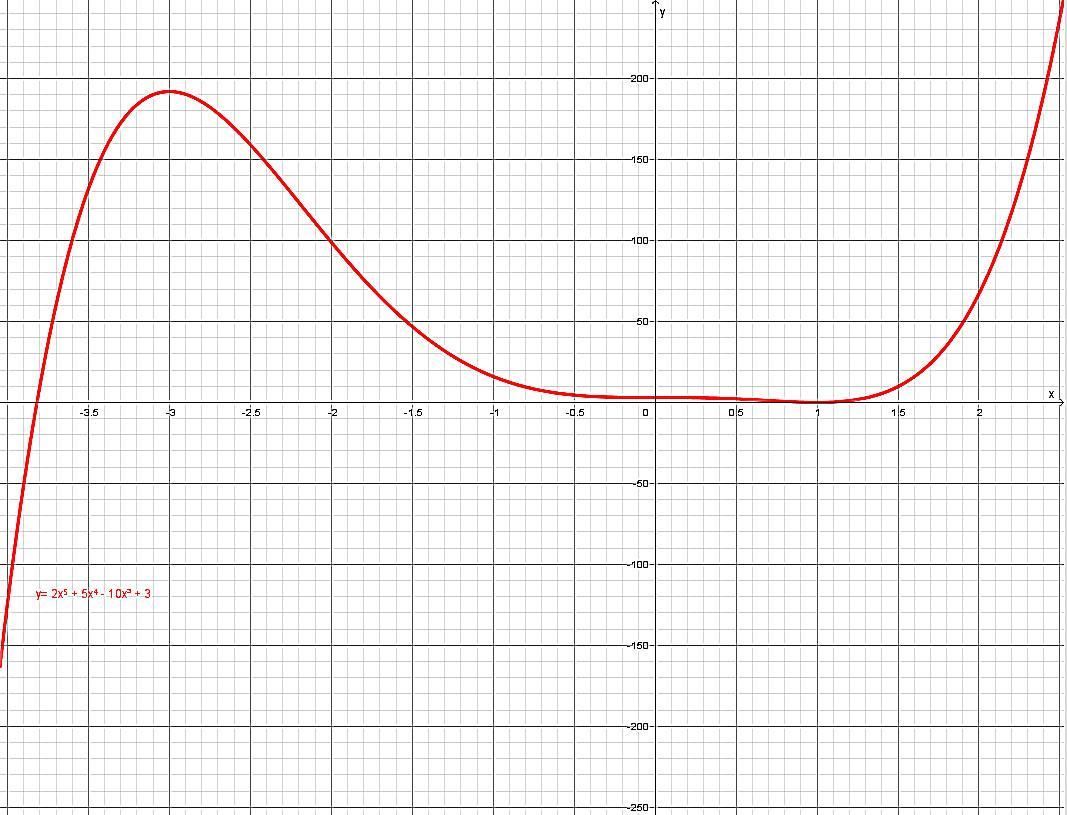
найдите промежутки возрастания и убывания функции y =2х^5 +5х^4-10х^3+3
Ответы
Ответ:Функция убывает при х∈(-3;0)U(0;1) Функция возрастает при х∈(-∞;-3)U(1;+∞)
Пошаговое объяснение:
найдите промежутки возрастания и убывания функции y=2х⁵+5х⁴-10х³+3
Решение
Решение Находим производную функции
y' = (2х⁵ + 5х⁴- 10х³ + 3)' = (2x⁵)' + (5x⁴)' - (10x³)' + 3'= 10x⁴ + 20x³ - 30x² =
= 10x²(x² + 2x - 3) = 10x²(x - 1)(x + 3)
Находим критические точки приравняв вторую производную к нулю y" = 0 ⇔ 10x²(x - 1)(x + 3) = 0
x₁ = -3 x₂ = 0 x₃ = 3
Отобразим на числовой прямой эти точки и найдем знаки производной по методу подстановки. Например при х = -1 10x²(x - 1)(x + 3) = -40 < 0
+ 0 - 0 - 0 +
------------------!-----------------!-------------------!-------------------
-3 0 1
Производная отрицательна и функция убывает
при x∈(-3 ; 0)U(0;1);
Производная положительна и функция возрастает
при x∈(-∞;-3)U(1;+∞).
В точке х = -3 y = 192 производная меняет свой знак с + на - поэтому функция имеет локальный максимум.
В точке х = 1 y = 0 производная меняет свой знак с - на + поэтому функция имеет локальный минимум.
График функции во вложении