Предмет: Алгебра,
автор: norman495
Решите эти уравнения, пожалуйста
Приложения:
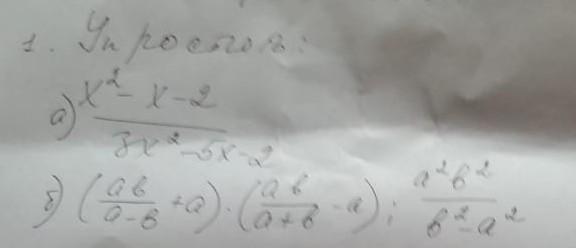
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Химия,
автор: mahdasja
Предмет: История,
автор: evadolgopolova6
Предмет: Математика,
автор: uvalieva04
Предмет: Математика,
автор: ирин6