Предмет: Геометрия,
автор: skrukov
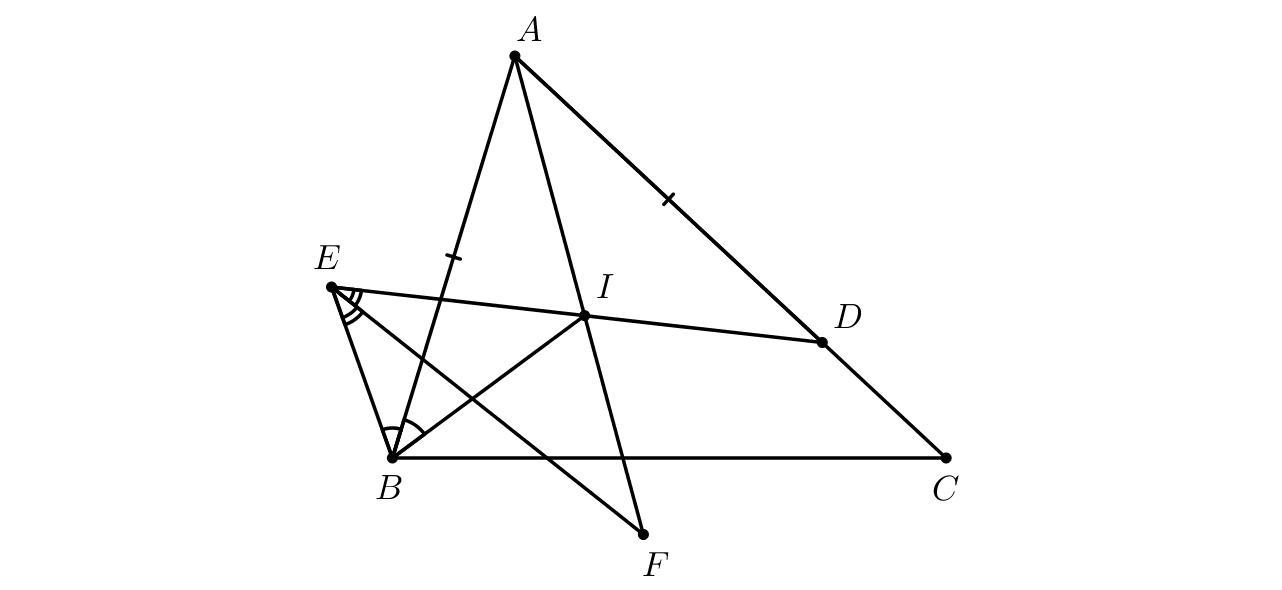
В треугольнике ABC на стороне AC выбрана точка D так, что AB=AD. I — центр вписанной окружности треугольника ABC. На луче DI выбрана точка E такая, что луч BA является биссектрисой угла IBE. Биссектриса угла BEI пересекает прямую AI в точке F. Выберите несколько точек, 3 из которых являются вершинами треугольника, а остальные — его центром (или центрами) вневписанной окружности (окружностей).
Приложения:
Ответы
Автор ответа:
7
Биссектрисы двух внешних углов и внутреннего угла треугольника пересекаются в центре вневписанной окружности.
Центр вписанной окружности треугольника (I) является точкой пересечения биссектрис, AI - биссектриса ∠BAC
△BAI=△DAI (по двум сторонам и углу между ними)
∠BIF=∠DIF (смежные с равными)
AF - биссектриса внешнего угла ∠BID треугольника BEI
EF - биссектриса внутреннего угла ∠BEI
F - центр вневписанной окружности △BEI
BA - биссектриса внутреннего угла ∠EBI треугольника BEI
A - центр вневписанной окружности △BEI
Приложения:

Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: dnmonexe
Предмет: Українська література,
автор: demvasia
Предмет: Физика,
автор: muzankovLife
Предмет: Химия,
автор: лола132