Question

Дана функция
$y = \frac{2.5 |x| - 1}{ |x| - 2.5 {x}^{2} }$
При каких значения k прямая y=kx не имеет с графиком ни одной общей точки​

Answer 1

$y=\dfrac{2,5|x| - 1}{|x| - 2,5x^{2}}$

Тут рационально написать так: $x^{2} = |x|^{2}$

Напишем ОДЗ функции:

$|x| - 2,5|x|^{2} \neq 0; \ |x|(1 - 2,5|x|) \neq 0; \ x \neq 0; \ x \neq \pm0,4$

Упростим функцию:

$y=\dfrac{2,5|x| - 1}{|x| - 2,5|x|^{2}} = \dfrac{2,5|x| - 1}{|x|(1 - 2,5|x|)} = -\dfrac{2,5|x| - 1}{|x|(2,5|x| - 1)} = -\dfrac{1}{|x|}$

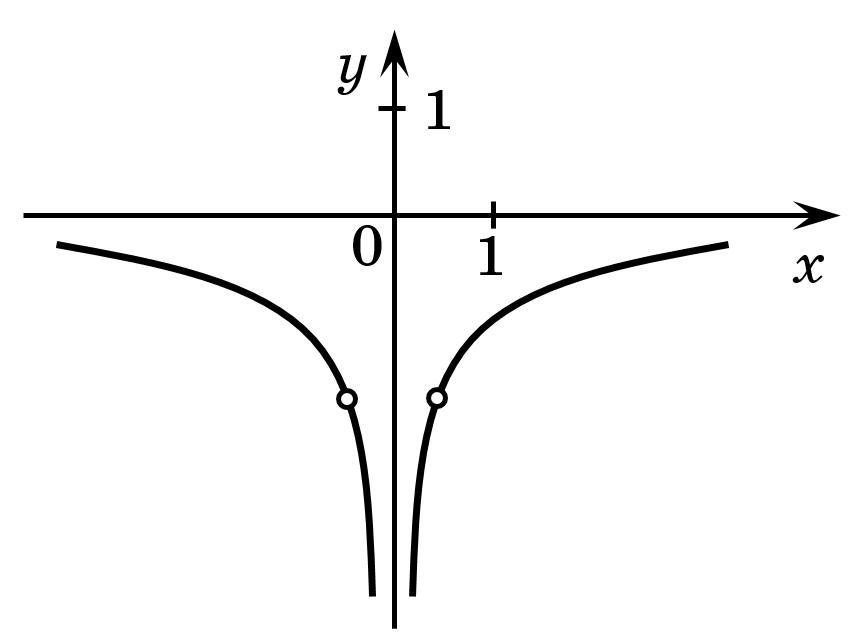
Нарисуем график этой функции (на месте ОДЗ точки выколоты). (Рисунок строем таблицей; рисунок схематический.)

Функция $y = kx$ — это прямая, проходящая через начало координат. С данным графиком она не будет имеет общих точек в 3 случаях:

• случаи, когда проходит через выколотые точки (их две);
• когда коэффициент $k$ равен нулю.

Если $x = \pm 0,4$, то $y = -2,5$. Отсюда: $-2,5 = 0,4k; \ k = -6,25; \ -2,5 = -0,4k; \ k = 6,25$

Ответ: прямая $y = kx$ не будет иметь с графиком функции $y=\dfrac{2,5|x| - 1}{|x| - 2,5x^{2}}$ не одной общей точки при $k = \pm 6,25$ и $k = 0$