Question

ПОМОГИТЕ ПОЖАЛУЙСТА!ДАЮ 50 БАЛЛОВ!
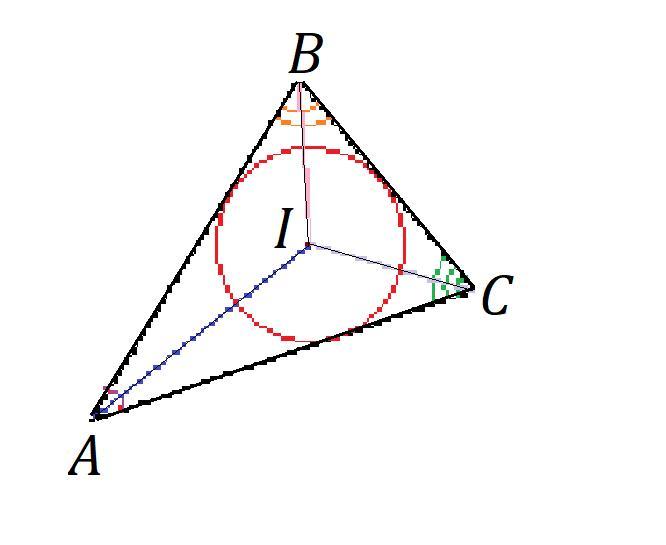
Точка I — центр вписанной окружности треугольника ABC. Известно, что ∠A=64∘, ∠B=32∘. Чему равны следующие углы?

∠BIC ∠AIB

Answer 1

Ответ:

132°, 122°.

Объяснение:

1) По теореме о сумме углов треугольника, ∠C = 180° - (∠A + ∠B) = 180° - (64° + 32°) = 84°.

2) Центр вписанной окружности - точка пересечения биссектрис.

⇒ AI - биссектриса ∠A, CI - биссектриса ∠C, BI - биссектриса ∠B.

3) Рассмотрим ΔAIB:

Из 2) ⇒ ∠BAI = ∠A : 2 = 64° : 2 = 32°, ∠ABI = ∠B : 2 = 32° : 2 = 16°.

По теореме о сумме углов треугольника, ∠AIB = 180° - (∠BAI + ∠ABI) = 180° - (32° + 16°) = 132°.

4) Рассмотрим ΔBIC:

Из 2) ⇒ ∠IBC = ∠B : 2 = 32° : 2 = 16°, ∠ICB = ∠C : 2 = 84° : 2 = 42°.

По теореме о сумме углов треугольника, ∠BIC = 180° - (∠IBC + ∠ICB) = 180° - (16° + 42°) = 122°.